beniamin
- 3
- 0
Homework Statement
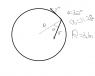
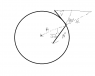
An object is constrained to move in a circular path of radius r = 3.1 m. At the instant diagrammed in the Figure 1, the directions of the velocity and acceleration are indicated by the v and a, respectively.The magnitude of the acceleration is a = 11.2 m/s^2 and the angle shown is θ = 32.
Homework Equations
a) What is the centripetal acceleration of the object?
b) What is the speed of the object?
c)What is the tangential acceleration of the object?
d) Is the speed increasing or decreasing? Explain.
The Attempt at a Solution
a = ac + at
Attachments
Last edited: