etotheipi
Please see the below diagram. I make the assumptions that the orbit of Jupiter around the sun is fairly unimportant for this problem, and that the period of Io is also much smaller than that of the Earth. I also assume everything is nice and circular and in the same plane.
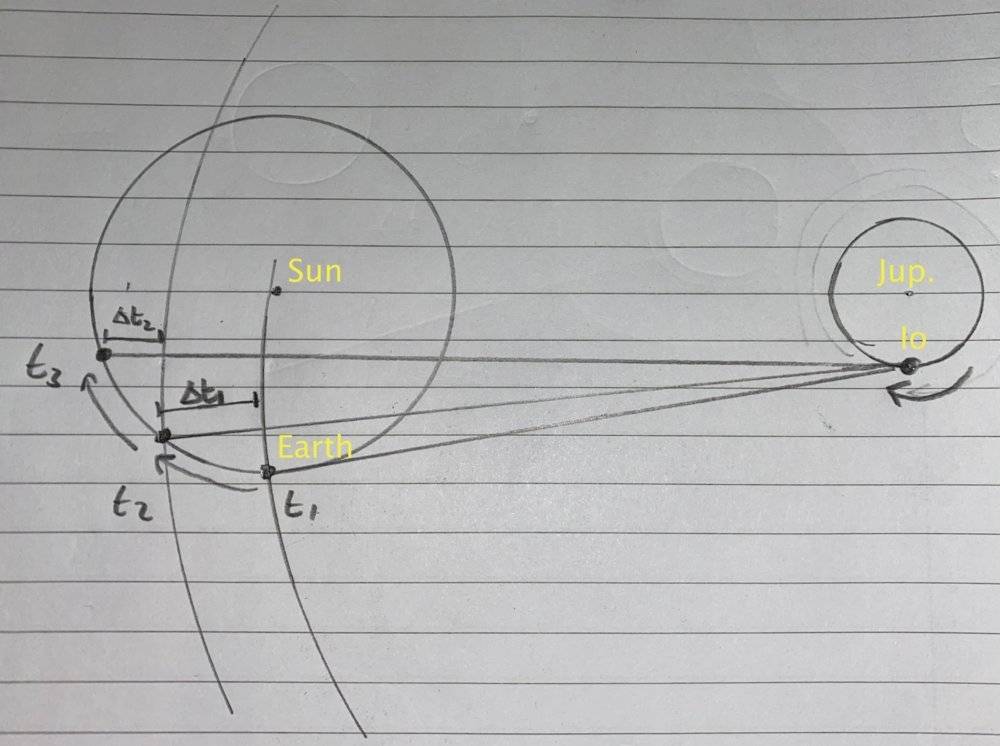
The intervals between observations of eclipses are greater than average on traveling away from Jupiter, and smaller than average when traveling toward Jupiter. The average ##T_{Io}## could then be calculated over a whole year.
I now consider the half-cycle period during which Earth travels exclusively away from Jupiter. Suppose light is emitted from an eclipse at absolute ##t=0##, which arrives at Earth at ##t = t_{1}##. The absolute time at which light from the second eclipse reaches Earth, ##t_{2}##, is ##t_{2} = T_{Io} + t_{1} + \Delta t_{1}##, where ##\Delta t_{1}## is the extra time the light needs to cover the slightly increased distance. Likewise, the absolute time at which light from the third eclipse reaches Earth is ##t_{3} = 2T_{Io} + t_{1} + \Delta t_{1} + \Delta t_{2}##.
The two intervals between successive detections are then ##T_{Io} + \Delta t_{1}##, and then ##T_{Io} + \Delta t_{2}##, and this pattern would continue onward like so.
Now over a half cycle of Earth's orbit, if the speed of light were infinite, we would expect the absolute time elapsed to be an integer multiple of ##T_{Io}##. However, the final eclipse actually will occur later by ##\Delta t_{1} + \Delta t_{2} + ...##, which Romer measured to be about 22 minutes.
This sum of time increments is supposed to represent the time for light to traverse the diameter of Earth's orbit, and whilst this seems somewhat reasonable (I've sketched some loci on the diagram), I can't find a rigorous way of showing that this sum does indeed converge to the diameter. I was wondering how I could go about finishing this off?
N.B. In the diagram I have put ##t_{1}## at an arbitrary point so that the lines are clearer, but evidently from what I have described it should be at the right-most point of Earth' orbit.
The intervals between observations of eclipses are greater than average on traveling away from Jupiter, and smaller than average when traveling toward Jupiter. The average ##T_{Io}## could then be calculated over a whole year.
I now consider the half-cycle period during which Earth travels exclusively away from Jupiter. Suppose light is emitted from an eclipse at absolute ##t=0##, which arrives at Earth at ##t = t_{1}##. The absolute time at which light from the second eclipse reaches Earth, ##t_{2}##, is ##t_{2} = T_{Io} + t_{1} + \Delta t_{1}##, where ##\Delta t_{1}## is the extra time the light needs to cover the slightly increased distance. Likewise, the absolute time at which light from the third eclipse reaches Earth is ##t_{3} = 2T_{Io} + t_{1} + \Delta t_{1} + \Delta t_{2}##.
The two intervals between successive detections are then ##T_{Io} + \Delta t_{1}##, and then ##T_{Io} + \Delta t_{2}##, and this pattern would continue onward like so.
Now over a half cycle of Earth's orbit, if the speed of light were infinite, we would expect the absolute time elapsed to be an integer multiple of ##T_{Io}##. However, the final eclipse actually will occur later by ##\Delta t_{1} + \Delta t_{2} + ...##, which Romer measured to be about 22 minutes.
This sum of time increments is supposed to represent the time for light to traverse the diameter of Earth's orbit, and whilst this seems somewhat reasonable (I've sketched some loci on the diagram), I can't find a rigorous way of showing that this sum does indeed converge to the diameter. I was wondering how I could go about finishing this off?
N.B. In the diagram I have put ##t_{1}## at an arbitrary point so that the lines are clearer, but evidently from what I have described it should be at the right-most point of Earth' orbit.
Last edited by a moderator: