Clebsch-Gordan coeffs, special cases

[Jesssa]

Hello,

I'm not sure whether I should have posted this in main Quantum mechanics thread because it's not really regarding homework, but I posted it in here just to be safe.

I was wondering, is there a way to derive the expression for these coefficients without the use of the general CGC formula?

For example, the J=0 case (this is taken from wikipedia)

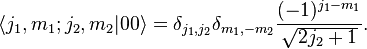
The 1/sqrt term is clear but the (-1)^.. term not so much, is there a way to find this coefficient?

I have read it requires the use of spinors and so on but I was wondering if there was a more simple way?

I found only a derivation of the CGC using only binomial expansions, but it was difficult to see exactly how they saw the starting point, it seemed like it must have been educated guesses until worked.

Thanks,

 

[HallsofIvy]

Perhaps I am misreading this, since you mention spinors, but aren't $j_1$ and $m_1$ simply integers? If so then $(-1)^{j_1- m_2)$ is +1 if [iterx]j_1[/itex] and $m_1$ have the same parity (both even or both odd) and +1 if they have different parity.

 

[Jesssa]

Thanks for replying HallsofIvy,

I understand what you have posted, but do you know how you get the (-1)^{j_1- m_1} term in the expression? I know, if you consider the formula it comes from the Wigner 3-j but I'm interested in finding out where it comes from (intuitively, if it is possible).

When I first saw the state, intuitively I saw the normalization factor 1/sqrt.. but I didn't expect/understand where the (-1)^{j_1- m_1} was coming from.