mohabitar
- 140
- 0
How were they able to derive this?
The sequence in this sum is a geometric sequence.mohabitar said: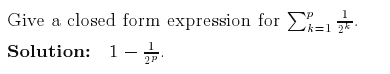
How were they able to derive this?
mohabitar said:None, I really don't see what you did from the 2nd step to the third step.
mohabitar said:Why would we subtract 1/2sp from sp? Can we just make a quick generalization? There was a trick to it that I forgot. If the summation starts at 1 and you want it to start at 0, then just take out the first term, or something like that? But now I still don't get the original question. Any other way to explain-you guys are really complicating this thing.