- #1
purpleBlob
- 10
- 0
I have some cubic box with light bulbs controlled by a dimmer. The dimmer is calibrated in degrees (0-270).
I need help in coming up with a function that would accurately predict what the temperature inside the box would be after say.. 5 or 10 minutes.
Basically, I need to come up with a function that would predict the temperature of the box after t (time) for a certain angle of the dimmer.
I think this would involve two variables (the dimmer's angle and the time interval). I have no idea though how to come up with an equation. I'm quite familiar with differential and integral calculus with same basic knowledge of multivariable calculus.
My question is very similar to this: (http://math.stackexchange.com/questions/11502/find-formula-from-values) except mine involves two variables and is definitely not linear.
Any tips?
----------
Here's a sample of the data I got from my 'calibration' experiment
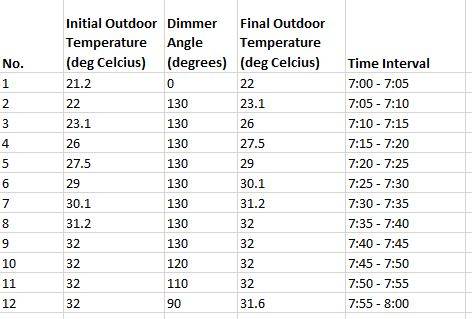
Where:
Init. Temp is the temperature at the start of the interval
Final. Temp is the temperature at the start of the interval
so the function would look something like this?: f(Ti, θ) = Tf
I could go on with the calibration so I can come up with a more accurate function but I simply want to know the general idea of how to come up with a function given some values.
-----
Thanks in advance!
I need help in coming up with a function that would accurately predict what the temperature inside the box would be after say.. 5 or 10 minutes.
Basically, I need to come up with a function that would predict the temperature of the box after t (time) for a certain angle of the dimmer.
I think this would involve two variables (the dimmer's angle and the time interval). I have no idea though how to come up with an equation. I'm quite familiar with differential and integral calculus with same basic knowledge of multivariable calculus.
My question is very similar to this: (http://math.stackexchange.com/questions/11502/find-formula-from-values) except mine involves two variables and is definitely not linear.
Any tips?
----------
Here's a sample of the data I got from my 'calibration' experiment
Where:
Init. Temp is the temperature at the start of the interval
Final. Temp is the temperature at the start of the interval
so the function would look something like this?: f(Ti, θ) = Tf
I could go on with the calibration so I can come up with a more accurate function but I simply want to know the general idea of how to come up with a function given some values.
-----
Thanks in advance!
Attachments
Last edited:

