QuantumRose
- 11
- 1
Here is the question:
By using the equality (for boson)
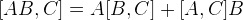 ---------------------------------------- (1)
---------------------------------------- (1)
Prove that
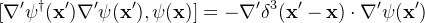
Background:
Currently I'm learning things about second quantization in the book "Advanced Quantum Mechanics"(Franz Schwabl).
Given the creation and annihilation operators(
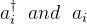 ), define field operators as
), define field operators as
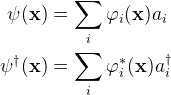
The following 3 commutator relations are for Boson.
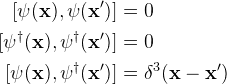 -----------------------------------(2)
-----------------------------------(2)
And here is my attempt (but it doesn't work):
First step, using equality (1) to expand the commutator:
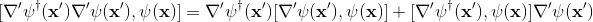 -------------(3)
-------------(3)
since the nabla operator is an operator, so I think the first term of (3)'s right-hand-side can be expressed as following
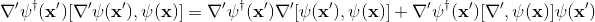
also, I expressed the second term of (3)'s right-hand-side by using the same method
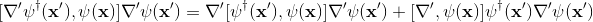
So, by inserting those commutators in (2), I found
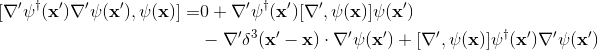
By using the equality (for boson)
Prove that
Background:
Currently I'm learning things about second quantization in the book "Advanced Quantum Mechanics"(Franz Schwabl).
Given the creation and annihilation operators(
The following 3 commutator relations are for Boson.
And here is my attempt (but it doesn't work):
First step, using equality (1) to expand the commutator:
since the nabla operator is an operator, so I think the first term of (3)'s right-hand-side can be expressed as following
also, I expressed the second term of (3)'s right-hand-side by using the same method
So, by inserting those commutators in (2), I found
Last edited: