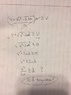ruskointhehizzy
Homework Statement
You are at a stoplight when you see a car approaching from behind at constant velocity. To avoid getting rear-ended, you accelerate forward with constant acceleration. Assume that you have managed to start at the last possible instant to avoid getting hit, as determined by the oncoming car's speed and your car's acceleration. How far behind you is the other car when you begin to move?
known: no values are given.
variables: velocity and acceleration.
Homework Equations
x = vt, v = at, Vx = dr/dt where r is displacement.
ax = dVx/dt or d^2r/dt.
x velocity: Vx = V0x + axt
position: x = x0 + Vx0t + 1/2axt^2
The Attempt at a Solution
I was driving today and I looked in my rear view and thought about this, as the car comes closer it is speeding up, as it becomes more distant it is slowing down. Then I tried thinking about this problem and don't know how to think about this. Honestly I don't even know where to start, I asked about 10 other students in class and they didn't either. If I could have someone here ask me relevant questions that will help me think this through I would greatly appreciate that. Please do not just give me the answer but help me think it though and derive it - I want to understand the concepts being taught in this problem. Thank you so very much!