Computing angular speed wrt CM I get a contradiction

[arestes]

Hello!
I have been brushing up my Rigid Body Dynamics.
I tried computing the angular speed with respect the Center of Mass (CM) using the usual split of kinetic energy and also the split of Angular momentum using the CM.
First, a simple case: Two particles of mass M each separated by a distance 2R. One going to the positive x direction with speed v and the other at rest.

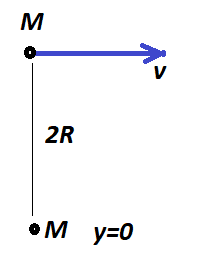
The Kinetic Energy, computed separately is:
KE=\frac{1}{2} M v^2
whereas the same KE computed using the split:
KE=\frac{1}{2} (2M) (v/2)^2 + \frac{1}{2} I_{CM} \omega_{CM}^2
Where, obviously, the speed of the CM is \frac{v}{2}. Also, it's easy to see that I_{CM} =2MR^2
therefore, equation both expressions for KE:
\omega_{CM} = \pm \frac{v}{2R}

Then, to check, I compute the angular momentum of the system (with respect to the point where the particle in rest is), using the same trick of splitting it using the CM (which clearly is exactly in the middle, at a distance R of each particle):
Separately: L_O=-Mv(2R)
As a system: L_O=-MvR+ I_{CM}\omega_{CM}=-MvR+(2MR^2)\omega_{CM}
Equating both expressions I get the right answer expected (this time with the correct sign):
\omega_{CM} = - \frac{v}{2R}

So far so good. Now comes the problem. I repeat the ordeal this time with a disk moving with speed v to the right but rotating with angular speed \omega_0. The CM is again exactly in the middle of the particle at rest and the center of the disk.

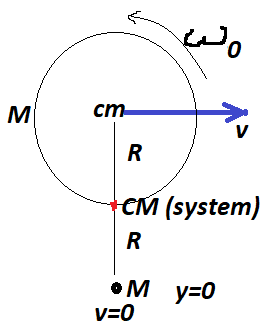
The Kinetic Energy of the system, computed separately (KE of the disk + 0 of the particle at rest):
KE=\frac{1}{2}Mv^2+\frac{1}{2} I_{0} \omega_0^2=\frac{1}{2}Mv^2+\frac{1}{2}(\frac{1}{2}MR^2 )\omega_0^2 =\frac{1}{2}Mv^2+\frac{1}{4}MR^2\omega_0^2
where I_{0} is just the moment of inertia of the disk wrt to its own cm, not of the system. Now I compute the same KE using the split and the CM:
KE=\frac{1}{2} (2M) (v/2)^2 + \frac{1}{2} I_{CM} \omega_{CM}^2=\frac{1}{2} (2M) (v/2)^2 + \frac{1}{2} (MR^2+(\frac{1}{2}MR^2+MR^2)) \omega_{CM}^2=\frac{1}{2} (2M) (v/2)^2 + \frac{1}{2} (\frac{5}{2}MR^2) \omega_{CM}^2=\frac{1}{4} M v^2 + \frac{5}{4} (MR^2) \omega_{CM}^2
using the parallel axis theorem (terms in parentheses) for the moment of inertia of the disk.
Equating both expressions I solve for \omega_{CM}
\omega_{CM}=(\frac{1}{5}((v/R)^2+\omega_0^2))^{1/2}

Something already seems odd. A square root of a sum... I then check what the angular momentum split tells me. First the angular momentum computed separately. The disk + 0 of the particle at rest:
Separately: L_O=-Mv(2R) +(I_{CM} \omega_0)=-2MvR +(\frac{1}{2} M R^2 \omega_0)
As a system: L_O=-(2M)(v/2)R+ I_{CM}\omega_{CM}=-MvR+((\frac{1}{2}MR^2+MR^2)+MR^2)\omega_{CM} =-MvR+ I_{CM}\omega_{CM}=-MvR+(\frac{5}{2}MR^2)\omega_{CM}
Equating both expressions I get
\omega_{CM} =\frac{1}{5}(-(v/R)+\frac{1}{2}\omega_0)

And clearly it's a contradiction. What is the correct result for \omega_{CM}?
Any help to resolve this?

 

[mfb]

Then, to check, I compute the angular momentum of the system (with respect to the point where the particle in rest is), using the same trick of splitting it using the CM (which clearly is exactly in the middle, at a distance R of each particle):
Separately: L_O=-Mv(2R)

That is not the angular momentum in the CM system, where you have 2 particles of mass M at distance R moving with v/2 for a total of L=MvR.
It is the angular momentum around the lower object, for example, but that is a different quantity.

 

[arestes]

That is not the angular momentum in the CM system, where you have 2 particles of mass M at distance R moving with v/2 for a total of L=MvR.
It is the angular momentum around the lower object, for example, but that is a different quantity.

Yes, It is in fact the angular momentum around the lower mass (at the origin).
Then I compute the same angular momentum but viewed as a system, therefore (as a system) there's a moment of inertia and I understand that the angular momentum around any point (in particular, again around O) can be split into L (of the center of mass point) _(around the chosen point) + rotational L.

I still get the right answer in the case of the point particles but something is wrong when I put forth the second example.

 

[PeroK]

Yes, It is in fact the angular momentum around the lower mass (at the origin).
Then I compute the same angular momentum but viewed as a system, therefore (as a system) there's a moment of inertia and I understand that the angular momentum around any point (in particular, again around O) can be split into L (of the center of mass point) _(around the chosen point) + rotational L.

I still get the right answer in the case of the point particles but something is wrong when I put forth the second example.

I didn't read all your post, but two independent point masses don't form a rigid body. In a rigid body, by definition, the distance between any two points must remain fixed.