tsw99
- 33
- 0
It is neither a homework nor coursework problem, but I really want to know the solution.
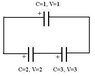
3 charged capacitors are connected as shown in the diagram. What will be their final charges, potential difference when equilibrium is reached? Units are arbitrary.
http://imageshack.us/photo/my-images/19/cap1zu.jpg
Q=CV obviously
(1) Should I use the charge conservation?
E.g. The total charge on left plates of C1 and C2 is 1+4=5 units, on right plate of C2 and left plate of C3 is -4+9=5 units, on right plates of C1 and C3 is -1-9=-10 units
(2) p.d. across C1 = p.d. across C2 and C3?
Equivalent capacitance across C2 and C3 = 1.2 unit
Then I cannot continue...
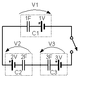
How about the case if the polarity of one of the capacitors is reversed? I feel really, really confused.
Homework Statement
3 charged capacitors are connected as shown in the diagram. What will be their final charges, potential difference when equilibrium is reached? Units are arbitrary.
http://imageshack.us/photo/my-images/19/cap1zu.jpg
Homework Equations
Q=CV obviously
The Attempt at a Solution
(1) Should I use the charge conservation?
E.g. The total charge on left plates of C1 and C2 is 1+4=5 units, on right plate of C2 and left plate of C3 is -4+9=5 units, on right plates of C1 and C3 is -1-9=-10 units
(2) p.d. across C1 = p.d. across C2 and C3?
Equivalent capacitance across C2 and C3 = 1.2 unit
Then I cannot continue...
How about the case if the polarity of one of the capacitors is reversed? I feel really, really confused.