JS-Student
- 10
- 0
Hi,
This is also a sort of geometry question.
My textbook gives a proof of the relation: sin(θ + Φ) = cosθsinΦ + sinθcosΦ.
It uses a diagram to do so:
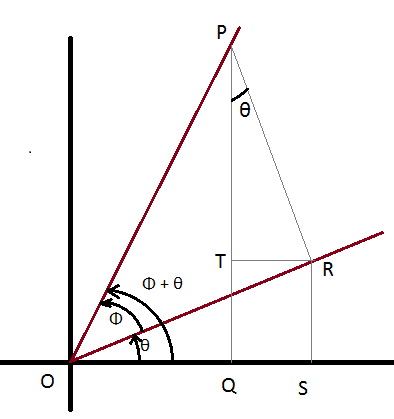
http://imgur.com/gLnE2Fn
sin (θ + Φ) = PQ/(OP)
= (PT + RS)/(OP)
= PT/(OP) + RS/(OP)
= PT/(PR) * PR/(OP) + RS/(OR) * OR/(OP)
= cosθsinΦ + sinθcosΦ
My confusion with this is
How do they know that angle TPR also measures θ?
How do they know that triangle TPR is similar to triangle ROQ?
Thanks
The textbook is: Calculus with Analytic Geometry, 2e by George F. Simmons
This is also a sort of geometry question.
My textbook gives a proof of the relation: sin(θ + Φ) = cosθsinΦ + sinθcosΦ.
It uses a diagram to do so:
http://imgur.com/gLnE2Fn
sin (θ + Φ) = PQ/(OP)
= (PT + RS)/(OP)
= PT/(OP) + RS/(OP)
= PT/(PR) * PR/(OP) + RS/(OR) * OR/(OP)
= cosθsinΦ + sinθcosΦ
My confusion with this is
How do they know that angle TPR also measures θ?
How do they know that triangle TPR is similar to triangle ROQ?
Thanks
The textbook is: Calculus with Analytic Geometry, 2e by George F. Simmons