Connection between Foucault pendulum and parallel transport

[Joker93]

Hello!

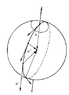
I try to think about the Foucault pendulum with the concept of parallel transport(if we think of Earth as being a perfect sphere) but I can't quite figure out what the vector that gets parallel transported represents(for example, is it the normal to the plane of oscillation vector?).

In particular, I can't exaplain the following animation https://en.wikipedia.org/wiki/File:Foucault_pendulum_plane_of_swing_semi3D.gif
which is found in this wikipedia article
https://en.wikipedia.org/wiki/Foucault_pendulum
using the concept of parallel transport.

Thanks in advance.

 

[pervect]

An object in free-fall would be a geodesic, which is related to parallel transport because a geodesic is just a curve that parallel transports it's own tangent vector.

You might look at https://arxiv.org/pdf/0805.1136.pdf. I havaen't really read it yet. My intuition is that we need Fermi-Walker trasnport, and not parallel transport, but I'm not sure if that's what the reference is saying.

 

[A.T.]

what the vector that gets parallel transported represents(for example, is it the normal to the plane of oscillation vector?).

In particular, I can't exaplain the following animation https://en.wikipedia.org/wiki/File:Foucault_pendulum_plane_of_swing_semi3D.gif

In the animation its obviously not the normal to the plane of oscillation, but a vector parallel to the oscillation plane and surface. But it doesn't really matter which vector you show, as they have a fixed 90° offset.

 

[Joker93]

In the animation its obviously not the normal to the plane of oscillation, but a vector parallel to the oscillation plane and surface. But it doesn't really matter which vector you show, as they have a fixed 90° offset.

That's what I thought at first but why does it get parallel transported in this way? At some points that vector is tangent to its trajectory, so wouldn't its parallel transport look something like the attached image?(from Do Carmo)

 

[Joker93]

An object in free-fall would be a geodesic, which is related to parallel transport because a geodesic is just a curve that parallel transports it's own tangent vector.

You might look at https://arxiv.org/pdf/0805.1136.pdf. I havaen't really read it yet. My intuition is that we need Fermi-Walker trasnport, and not parallel transport, but I'm not sure if that's what the reference is saying.

But is does not follow a geodesic since a geodesic on a sphere is a great circle.
Also, I do not know about Fermi-Walker transport. I will check out the pdf file though. Thanks!

 

[A.T.]

That's what I thought at first but why does it get parallel transported in this way?

https://en.wikipedia.org/wiki/Foucault_pendulum#Precession_as_a_form_of_parallel_transport

At some points that vector is tangent to its trajectory, so wouldn't its parallel transport look something like the attached image?(from Do Carmo)

No, for the reason you state yourself:

But is does not follow a geodesic..

 

[Joker93]

https://en.wikipedia.org/wiki/Foucault_pendulum#Precession_as_a_form_of_parallel_transportNo, for the reason you state yourself:

So, I guess my weak intuition betrayed me.
Thanks, now everything makes more sense!