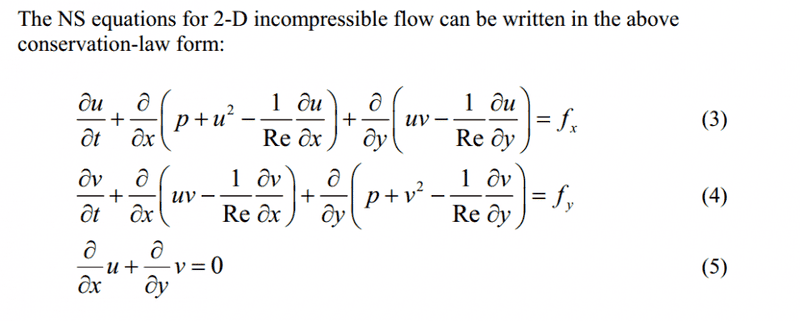SUMMARY
The discussion focuses on converting the Navier-Stokes Equation into conservation form. Key points include the elimination of the density term with the pressure gradient and the transformation of the term du^2/dx into u du/dx. The integration by parts method is employed to derive the equation, leading to the conclusion that the continuity equation simplifies the expression, confirming that u∂u/∂x + v∂u/∂y equals ∂u²/∂x + ∂(uv)/∂y.
PREREQUISITES
- Understanding of the Navier-Stokes Equation
- Familiarity with fluid dynamics concepts
- Knowledge of integration by parts in calculus
- Comprehension of the continuity equation in fluid mechanics
NEXT STEPS
- Study the derivation of the Navier-Stokes Equation in conservation form
- Learn about the implications of the continuity equation in fluid dynamics
- Explore advanced integration techniques in calculus
- Investigate applications of the Navier-Stokes Equation in real-world fluid flow scenarios
USEFUL FOR
Students and professionals in fluid dynamics, applied mathematicians, and engineers working on computational fluid dynamics (CFD) who require a solid understanding of the Navier-Stokes Equation and its applications.