Conservation of energy (and rotational kinetic engery)

[daivinhtran]

This is not a homework question.

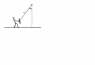
An adult exerts a horizontal force on a swing that is suspended by a rope of length L, holding it
at an angle θ with the vertical. The child in the swing has a weight W and dimensions that are negligible compared to L. The weights of the rope and of the seat are negligible.

Then the adult releases the swing from rest.
as the swing passes through its lowest point, does the system have rotational kinetic energy also?
(<-- this is my own question)
My teacher pulled up this question and ask everyone solve for v (when it reach the bottom)?

Is it like : initial Translational K + initial Potential U = final Translational K + final Potential U

OR : intial translational K + initial Potential U = final Translational K + final rotation K + final Potential U ??

At first, everyone thought the first way. BUt my teacher pull up the second thought, and it make perfect sense.

So, I look up the question online, and all scoring guidelines solve it without rotational kinetic energy.

WHO IS RIGHT AND WHO IS WRONG?

 

[daivinhtran]

Picture is attached

 

[bs15benny]

If your teacher asked you to find V of the swing, I think it is better to use free fall equation. Where h=0.5gt^2 and v=gt. This is because the adult only releases the swing not push it and let the swing to free fall.

 

[daivinhtran]

If your teacher asked you to find V of the swing, I think it is better to use free fall equation. Where h=0.5gt^2 and v=gt. This is because the adult only releases the swing not push it and let the swing to free fall.

this way doesn't work because different points of the swing have different velocity. They only have same rotational velocity.

 

[AlephZero]

Using the free fall equations is just wrong, because nothing is in free fall (vertically downwards) here!

I would say that in theory your teacher is right and you should include the rotational KE of the child on the swing.

But in practice, you don't have enough information to do that. You don't know the moment of inertia of the child about its CG, and you don't know its angular velocity either. (The angular velocity of the child isn't necessarily the same as the angular velocity of the swing about its pivot at the top. The child isn't a sack of potatoes, it can move around on its own!)

So the only way you can solve the problem is to ignore the rotational KE of the child. And if you make a sensible guess about the moment of inertia of the child, you will find it doesn't change the answer by much.

The important take home message here is: to do physics or engineering, you have to think about what you are doing.

 

[bs15benny]

oh if it is about rotational velocity, do you know the rotational acceleration? if you know it we can use the rotational acceleration equation.

 

[daivinhtran]

Using the free fall equations is just wrong, because nothing is in free fall (vertically downwards) here!

I would say that in theory your teacher is right and you should include the rotational KE of the child on the swing.

But in practice, you don't have enough information to do that. You don't know the moment of inertia of the child about its CG, and you don't know its angular velocity either. (The angular velocity of the child isn't necessarily the same as the angular velocity of the swing about its pivot at the top. The child isn't a sack of potatoes, it can move around on its own!)

So the only way you can solve the problem is to ignore the rotational KE of the child. And if you make a sensible guess about the moment of inertia of the child, you will find it doesn't change the answer by much.

The important take home message here is: to do physics or engineering, you have to think about what you are doing.

It's a very interesting problem. My teacher assumes that the moment of inertia of the child is MR^2

But it turn out the translational K = rotational K ==> total K = mv^2

And some other folks (big guys) said that my teacher is wrong
" What contributes to the total kinetic energy of the system? Clearly, the translational kinetic energy of the kid, 1/2 m v^{2} must be accounted for. But what about rotational kinetic energy of the kid about the center of the swing? Well, that's exactly the same motion we're trying to quantify with translational kinetic energy. So no, we shouldn't add this on again because it tells us exactly the same thing as 1/2 m v^{2} ! "
Honestly, I believe in these folks rather than my teacher.

ALso, thank you for your message :).

 

[bs15benny]

oh right... i just realized that if in rotation case.. the velocity is always changing and when the swing at the bottom the velocity is maximum. Honestly, I haven't learn about the translational and rotational kinetic energy. Sorry for the misunderstanding..