Conservation of Energy find the speed of the blocks

[uchicago2012]

Homework Statement

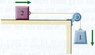
In the figure the second block slides horizontally without friction while the first block falls. Use the Conservation of Energy to find the speed of the blocks after they have moved 2 meters, starting from rest. The falling block has mass 3 kg, the sliding block has mass 5 kg, and the pulley is ideal.
See Figure 1.

Homework Equations

U_f + K_f = U_i + K_i

The Attempt at a Solution

So for the 3 kg block:
mgh_f = 1/2mv_f² = mgh_i + 1/2mv_i²
(3 kg)(9.8 m/s²)(2 m) + 1/2(3 kg)(v_f)² = 0
1/2(3 kg)(v_f)² = 58.8 J
(v_f)² = 39.2 m²/s²
v_f = 6.26 m/s

I'm not sure if I quite got the point of the conservation of energy bit. Does it mean the work done by the pulley is zero? That's what I had to assume to get v_f for the 3 kg block. I'm not sure what to do about the 5 kg block, though, because if I just use 2 m for the h for it, then I get the same v_f as the 3 kg block, which seems odd to me. But maybe I'm missing the point.

 

[ehild]

The pulley exerts a force on the rope and it is perpendicular to the rope. No work is involved by the pulley.

The change of the potential energy is equal to that of the falling block, but does it increase or decrease?

The blocks move together with the same speed. The total KE of the system is the sum of the KE-s of both blocks.

ehild