Conservation of Energy in Conjunction With Momentum

[Bashyboy]

Homework Statement

Consider an elastic collision between two bodies of equal mass, one of which is initially at rest. Let their velocities be \vec{v_1} and \vec{v_2} = \vec{0} before the collision, and \vec{v_1 '} and \vec{v_2 '} after the collision. Write down the vector equation representing conservation of momentum and the scalar equation which expresses that the collision is elastic. Use these to prove that \vec{v_1 '} and \vec{v_2 '} are orthogonal.

Homework Equations

The Attempt at a Solution

If the collision is elastic, then KE = KE'.

m1 = m2 = m

\vec{p} = \vec{p'}

If the two velocity vectors are orthogonal, then \vec{v_1 '} \cdot \vec{v_2 '} = 0.

Conservation of energy:

\frac{1}{2} mv_1^2 = \frac{1}{2} m v_1^{'2} + \frac{1}{2} m v_2^{'2}

v_1^2 = v_1^{'2} + v_2^{'2}, which can be written as | \vec{v_1} |^2 =| \vec{v_1 '} |^2 + | \vec{v_2 '} |^2, although I am not sure of how helpful this will be.

Conservation of momentum:

m \vec{v_1} + \vec{0} = m \vec{v_1 '} + m \vec{v_2 '}

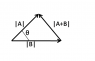
\vec{v_1} = \vec{v_1 '} + \vec{v_2 '}

Taking the magnitude, | \vec{v_1} | = | \vec{v_1 '} |+ | \vec{v_2 '} |; again, I am not certain of how helpful this will be.

______________________________________________________

Up to this point, I am not sure as to how to proceed. Could someone provide me with a hint?

 

[Saitama]

Hi Bashyboy!

Taking the magnitude, | \vec{v_1} | = | \vec{v_1 '} |+ | \vec{v_2 '} |; again, I am not certain of how helpful this will be.

Nooo.

$|\vec{v_1}|=| \vec{v_1 '} + \vec{v_2 '} | ≠ | \vec{v_1 '} |+ | \vec{v_2 '} |$.

 

[Bashyboy]

Yes, of course. I actually have the correct expression on my paper, but somehow I failed to properly type it up.

 

[Saitama]

Yes, of course. I actually have the correct expression on my paper, but somehow I failed to properly type it up.

Well...$|\vec{v_1'}+\vec{v_2'}|$ means the magnitude of resultant of $\vec{v_1'}$ and $\vec{v_2'}$. Can you proceed further?

 

[Bashyboy]

Well, I now have that | \vec{v_1} | = | \vec{v_r '} |, and I also have that |\vec{v_1}|^2 = | \vec{v_1 '} |^2 + | \vec{v_2 '}|^2. I am to make some sort of substitution?

 

[Saitama]

Well, I now have that | \vec{v_1} | = | \vec{v_r '} |, and I also have that |\vec{v_1}|^2 = | \vec{v_1 '} |^2 + | \vec{v_2 '}|^2. I am to make some sort of substitution?

If two vectors, $\vec{A}$ and $\vec{B}$ make an angle $\theta$ with each other, what is the magnitude of resultant of the two vectors?

 

[Bashyboy]

I don't quite follow. I have never seen the sum of two vectors in terms of their angle.

 

[Saitama]

I don't quite follow. I have never seen the sum of two vectors in terms of their angle.

I don't know how it is at your place but that's something taught at the very beginning here.

Okay, if you haven't seen it, you can use cosine rule to derive it. Draw a vector diagram.

 

[Bashyboy]

No, I would much rather see your method, please.

 

[Saitama]

No, I would much rather see your method, please.

Apply cosine rule to the triangle shown in the attachment.

 

[Bashyboy]

When you say cosine rule, do you also mean the law of cosines? The law of cosines for vectors is simply the dot product, is it not?

 

[Saitama]

When you say cosine rule, do you also mean the law of cosines? The law of cosines for vectors is simply the dot product, is it not?

Yes, very sorry, it is the law of cosines. I am used to calling it the "cosine rule".

To avoid confusion, I am talking about this: http://mathworld.wolfram.com/LawofCosines.html

 

[Bashyboy]

So, you are suggesting that by solving the law of cosines for theta, it will equal 90 deg.?

 

[Saitama]

So, you are suggesting that by solving the law of cosines for theta, it will equal 90 deg.?

You can see it yourself. Apply the law of cosines. Show your work.

 

[Bashyboy]

Sorry it took awhile to reply. Well, after applying the Law of Cosines, the problem became rather trivial: it's all a matter of memorizing those tricks and formulas of mathematics. At any rate, Pranav-Arora, I thank you very much for time.

 

[Saitama]

Sorry it took awhile to reply. Well, after applying the Law of Cosines, the problem became rather trivial: it's all a matter of memorizing those tricks and formulas of mathematics. At any rate, Pranav-Arora, I thank you very much for time.

Glad to help. :)