zorro
- 1,378
- 0
See the figure-
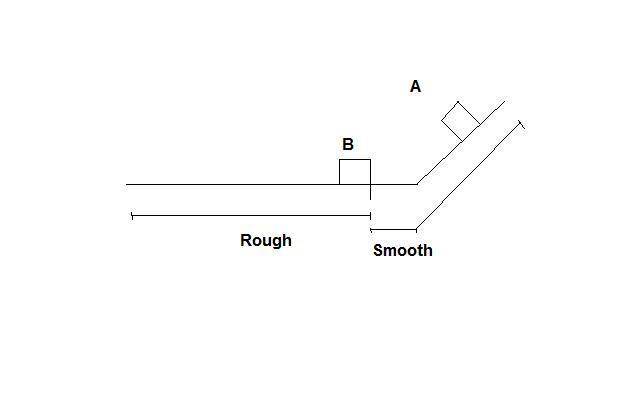
The block A collides inelastically with the block B. I have seen in 2 of my books that they apply conservation of momentum in such problems along x-direction. According to me, since there is an external frictional force acting, the linear momentum is not conserved.
Is it that they consider Earth + A + B to be the system and ignore the velocity of the Earth ?
Please throw some light on this.
The block A collides inelastically with the block B. I have seen in 2 of my books that they apply conservation of momentum in such problems along x-direction. According to me, since there is an external frictional force acting, the linear momentum is not conserved.
Is it that they consider Earth + A + B to be the system and ignore the velocity of the Earth ?
Please throw some light on this.

 ).
).