Constant Current Source in Driving an RC Circuit

[Abdullah Almosalami]

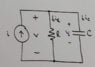
Alright. So I'm getting two different solutions depending on how I look at this problem, and I know one is correct but I don't know why the other would be incorrect. So, given this general circuit of a constant current source driving an RC circuit in parallel:

Now, what they tell me in class is that this is a DC source, so after transients have gone, the capacitor will be an open circuit, so v should just be i*R. And indeed in simulation, this is what I get. However, if I do try to apply KCL and solve for V, without knowing that say after transients the capacitor will be essentially an open circuit, I get my two different solutions:

- If I keep the circuit as it is and attempt to solve for v, I get the following:

You can see at the very bottom there, I get v(t) = iRC + (vc0 - iRC)exp((-1/RC)t). This converges to iRC! Not iR as I'm expecting. I'm not sure if I did a mathematical error in there somewhere, but as of right now, I can't tell.

- If I source transform the the current source in parallel with the resistor to a voltage source in series with a resistor, then I get:

This version will indeed converge to iR. And I know this must be correct, so what happened?

 

[Abdullah Almosalami]

Ok so literally right after posting, I realized what went wrong. The differential equation up top in the second photo should have i/C as the forcing function, not just i. I missed that part when dividing out C. Redoing the work, both version do match and I'm an idiot:

 

[jrmichler]

version do match and I'm an idiot

Well, no. Asking for help means that you have to lay out the problem for another person. When you do that, you are looking at the problem from a different direction, which frequently leads to the solution.

Part of my last job was helping other engineers solve difficult problems. It was common for somebody to come into my office, start writing on the dry erase board, then say "Oops, got it now".

 

[berkeman]

Part of my last job was helping other engineers solve difficult problems. It was common for somebody to come into my office, start writing on the dry erase board, then say "Oops, got it now".

Wait, when was I in your office?

 

[analogdesign]

Well, no. Asking for help means that you have to lay out the problem for another person. When you do that, you are looking at the problem from a different direction, which frequently leads to the solution.

This is such a common and powerful technique that people now do it alone, and there is a funny name for it and everything: https://en.wikipedia.org/wiki/Rubber_duck_debugging

In a slightly related vane, my PhD advisor often would say that you didn't understand something until you could explain it to your grandma. We had a pretty good relationship and here is one of our actual conversations while I was writing my thesis:

Prof: You're over thinking this aspect of the algorithm and the exposition isn't clear. You need to try to think of a way to explain it to your grandma.

Me: My grandma's dead.

Prof: Get out of my office.

Good times.

 

[Abdullah Almosalami]

This is such a common and powerful technique that people now do it alone, and there is a funny name for it and everything: https://en.wikipedia.org/wiki/Rubber_duck_debugging

In a slightly related vane, my PhD advisor often would say that you didn't understand something until you could explain it to your grandma. We had a pretty good relationship and here is one of our actual conversations while I was writing my thesis:

Prof: You're over thinking this aspect of the algorithm and the exposition isn't clear. You need to try to think of a way to explain it to your grandma.

Me: My grandma's dead.

Prof: Get out of my office.

Good times.

That was freaken hilarious!

 

[AVBs2Systems]

Ok

Good work. I thought I might add three things which may help you appreciate why this hard work you did would be beneficial later:
$$ \text{The step response of RL, RC and other systems} $$
The response of such systems to step functions, basically DC waveforms that are switched on after some period of time, is of interest to engineers as the step response is quite closely related to the LTI systems impulse response. The dirac pulse and unit step are signals inserted into systems as your input waveforms to characterise the system. The step and impulse are related mathematically and in the frequency domain too. The step response for charging RL and RC circuits (zero initial conditions) is (with the appropriate physical units for voltage and current respectively):
$$ kg(t) = k \epsilon(t) \cdot \big( 1 - e^{-\frac{t}{\tau} } \big)$$
$$ \text{General equation to describe transient circuits} $$
If initial conditions are given, it is usually easier to use this for charging RL and RC circuits:

$$ x(t) = x \big[ t \to \infty \big] + \Big( x\big[ t =0 \Big] - x \big[ t \to \infty \big] \Big) e^{ -\frac{t}{\tau} } $$
$$ \text{The homogenous solution of the circuits differential equation and the forcing function } $$
Every differential equation consists of two parts, the homogenous solution and the particular solution.
$$ y(x) = y_{h}(x) + y_{p}(x) $$
The homogenous solution is the transient equation, the particular solution is the forcing function and steady state solution.