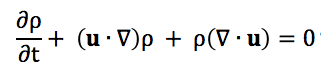Constant density vs Incompressible

[humphreybogart]

The continuity equation in fluid mechanics is:

Do the condition of "constant-density fluid' and 'imcompressible flow' have the same effect on the continuity equation, in that the first two terms disappear?

Or is there a difference between these assumptions?

 

[Mech_Engineer]

It seems to me the assumption in each case would be the same, in that you are assuming the density is constant. Whether this is because the fluid is incompressible, or because the flow is in a regime which doesn't cause significant density variations shouldn't matter.

https://en.wikipedia.org/wiki/Incompressible_flow

In fluid mechanics or more generally continuum mechanics, incompressible flow (isochoric flow) refers to a flow in which the material density is constant within a fluid parcel—an infinitesimal volume that moves with the flow velocity.

 

[bigfooted]

continuity equation:
$\frac{\partial \rho}{\partial t} +\nabla \rho \cdot u + \rho (\nabla \cdot u) = 0$
let's assume that $\rho = \rho(x,y,z)$ is constant in time :
$\nabla \rho \cdot u + \rho (\nabla \cdot u) =0$
let's assume that $\rho = \rho(t)$ is constant in space:
$\frac{\partial \rho}{\partial t} + \rho (\nabla \cdot u) = 0$
let's assume that $\rho$ is constant in time and space:
$\nabla \cdot u = 0$

If a flow is incompressible, we demand that an infinitesimal volume doesn't change its volume while it moves with the flow. This is equivalent to demanding that the divergence of the velocity is zero. So, if the density is constant in space and time, the flow is automatically divergence free and therefore incompressible. However, if the flow is divergence free, it does not automatically mean that the density is constant.

Let's assume that the flow is incompressible, :
$\frac{\partial \rho}{\partial t} +\nabla \rho \cdot u = 0$
This is the material derivative of density. Incompressible flow therefore is equivalent to flow with vanishing material derivative of density. Integration leads to the conclusion that the material density must be constant, which is different from the assumption that the physical density is constant.
Even if the density is constant in time, the density is still allowed to vary spatially in an incompressible flow. In a steady burning candle flame for instance, the flow is incompressible but the density is varying spatially.

To conclude: assuming constant density is different from assuming incompressibility; assuming constant density implies incompressibility but assuming incompressibility does not imply constant density.

 

[boneh3ad]

So, not to be overly contrarian here, but I don't entirely agree with the analysis of @bigfooted. While I do recognize that flow with low velocities and density variations do exist, I will contend that these are still compressible flows even though they obey the Mach number requirement for incompressible flows. At the bottom of this post are a list of references I have laying around that all cite $\rho=\mathrm{constant}$ as the defining characteristic of an incompressible flow. The references span a range of levels (undergraduate, graduate, etc.).

The reason I favor such a definition is that the incompressible assumption commonly carries with it a handful of implications. First, if you assume the density to be constant, you are left with 4 equations and 4 unknowns and it decouples the energy equation from the system, so there is no closure problem. Second, while it is not enforced, the assumption of constant density carries with it the assumption that temperature variations are either nonexistent or quite small (otherwise, the constant density assumption doesn't make a lot of sense in reality), so that also let's us make a number of simplifying assumptions on the momentum and energy equations, such as that the viscosity and the thermal conductivity are constants, which let's us keep our relatively tractable 4 equations.

Generally speaking, if you want to capture all of the physics of flows that have variable density, you simply have to use the full compressible Navier-Stokes equations and treat it as a compressible flow, even if the flow itself is low speed. However, it is fairly common to approximate such flows as incompressible to make the problem more tractable. Usually, in my experience, the approach in these situations is to assume the density variations are small and invoke the Boussinesq approximation. Usually that takes the form of assuming that, for reference (mean) values of $\rho$, $T$, and $p$, the deviations are small and a Taylor Expansion yields
\rho = \rho_{\infty} + \left(\dfrac{\partial \rho}{\partial T}\right)(T - T_{\infty}) + \left(\dfrac{\partial \rho}{\partial p}\right)(p - p_{\infty})+H.O.T..
Based on the values of these derivatives, this is often written as
\rho \approx \rho_{\infty} + \rho_{\infty}\beta(T - T_{\infty}) + \dfrac{\gamma}{c^2}(p - p_{\infty})
where $\beta$ is the coefficient of thermal expansion, $\gamma$ is the ration of specific heats, and $c$ is the speed of sound. As long as the speed is low and the pressure variations are therefore fairly small, that $c^{-2}$ term is generally very small, so in this limit, the density's dependence on pressure is effectively negligble. In that sense, you can transform the full compressible equations into a simpler set that retain many of the features of the incompressible equations, but it's still not truly an incompressible flow. For larger variations in density, other methods are necessary to avoid using the compressible equations.

The one text that I have that doesn't define incompressibility is http://amzn.com/0521663962 . He uses the following definition: "A fluid is said to be incompressible when the density of an element of fluid is not affected by changes in pressure." This is equivalent to saying that
\dfrac{D\rho}{Dt}=0
or
\nabla\cdot\vec{V} = 0,
that the velocity field is solenoidal. This is the same as what @bigfooted has done. However, in the same text, the author goes on to use scaling analysis to describe the situations in which this assumption holds, and it boils down to five different criteria.

First:
\dfrac{V^2}{c^2} \ll 1
This is the common criteria that the Mach number must be small, usually taken to be $M<0.3$ such that the above is more than an order of magnitude less than 1. This is violated in high speed aerodynamics and is probably the most commonly studied situation in which flows are compressible. This corresponds with the field of gas dynamics.

Second:
\dfrac{f^2 L^2}{c^2} \ll 1
This pertains to unsteady flows where $f$ is some dominant frequency involved with the unsteadiness, $L$ is the characteristic length of a flow being considered, and $c$ is as above. This is effectively a squared Strouhal number based on sound speed. However, it approaches unity when considering sound waves, where $L$ corresponds to the wavelength of an unsteady motion of speed $c$ and frequency $f$. In that case, the compressibility of the fluid (even liquids like water) is inherently important. This corresponds with the field of acoustics.

Third:
\dfrac{gL}c^2 \ll 1
This is a statement about body forces balanced by pressure distributions. He shows that this really can only ever be violated in gases like air, and that it boils down to a criteria for whether the scale of the flow is small compared to $p/(\rho g)$, which is called the scale height of the atmosphere and is something like 8+ km for air in our atmosphere. This criteria is violated in meteorology.

Fourth:
\dfrac{\beta U^2}{c_p}\dfrac{\mu}{\rho L U} \ll 1
where $\beta$ is the coefficient of thermal expansion, $\mu$ is the viscosity, and $c_p$ is the specific heat at constant pressure. This relates to viscous dissipation being small enough that it does not generate enough heat to affect the density. Given the nature of viscous dissipation, it is almost impossible for this to be a factor, and I don't know of any situations off the top of my head in which this would absolutely be violated.

Fifth:
\beta\theta\dfrac{\kappa}{LU} \ll 1
where $\kappa$ is the thermal diffusivity. This is a statement about heat conduction being small and not affecting the temperature enough to change the density. The only way this is violated is when you have a very high temperature gradient and/or small values of $LU$. The candle situation actually typically can violate this. There is an analogous term for flow in which there are concentration or species variations to cover mass transfer and its effect on compressibility as well.

So, with all of that in mind, I would argue that the candle situation is not incompressible in the strict sense of the term, and that $\rho$ being constant essentially covers all of the bases provided by Batchelor and is the better, more intuitive description for when a flow is incompressible.

Sources using $\rho=\mathrm{constant}$:
http://amzn.com/1118912659
http://amzn.com/1118116135
http://amzn.com/1259129918
http://amzn.com/0073398276
http://amzn.com/0072402318
http://amzn.com/3540662707

 

[bigfooted]

Again, a constant density flow means that it is an incompressible flow, but an incompressible flow does not mean that it is a constant density flow. Formally correct is: an incompressible flow is a flow where the compressibility factor is small, or where the material derivative of density vanishes, e.g. in the preview of chapter 2 here:
http://www.springer.com/gp/book/9783319315973
and some freely available lecture notes from MIT:
https://ocw.mit.edu/courses/materia...ngineering-fall-2003/study-materials/3_21.pdf.
and apparently in the book of Batchelor quoted above.

I checked some of the books mentioned above and I am relieved to find that these authors actually do not make the mistake to equate constant density flows and incompressible flows (although their wording could be easily misinterpreted).
White (viscous fluid flow) says: "if the density is constant(incompressible flow) , eq 2.6 [the continuity equation] reduces to the condition of velocity solenoidality."
Here, he is merely saying that a constant density flow is an incompressible flow, not that an incompressible flow is also a constant density flow.
Schlichting says a similar thing: "Consequently the flow of a gas can be considered incompressible when the relative change in density remains very small."
Unfortunately, Anderson makes a wrong statement when he says "A flow in which the density is constant is called incompressible and a flow where the density is variable is called compressible". I, and I think all my colleagues from the Combustion Institute, would beg to differ. Actually, later in the book he starts with the definition of the compressibility factor $\tau=\frac{1}{\rho}\frac{dp}{d\rho}$ and then derives the condition that the speed of sound can be written as $a=\sqrt{\frac{1}{\rho \tau}}$, showing that the Mach number should be small in incompressible flows.

I was looking for a nice reference that I could point to that shows the relationship between the velocity divergence and the criteria mentioned in Batchelor and above to make it more clear how they were derived, and the best derivation I could find was actually here on physicsforums (if somebody knows of a literature reference, please let me know):
https://www.physicsforums.com/threads/when-can-one-assume-incompressible-flow.129837/

And indeed, as was shown by Batchelor(see post above), Karamcheti and in the reference above, when the Reynolds number is low and temperature gradients are high, there can be compressibility effects in (laminar) reacting flows. Still, a candle flame can be modeled as an incompressible flame because the Laplacian of temperature is an order of magnitude smaller than the gradient of density. I do not know of anybody who simulates laminar flames with a compressible code though, unless there is considerable physical interaction with pressure waves. Actually, we have found it to be a very inconvenient thing to do because compressible codes tend to create artificial pressure waves which take a very long time to dissipate.
Instead of a candle flame, a better example of an incompressible varying-density flow would have been a turbulent flame, or simply the mixing of two gases with different densities.

 

[boneh3ad]

I am no longer in my office so I don't have most of my books with me to go flip back through them. However, I will concede that in Viscous Fluid Flow, he does indeed cite constant density as a sufficient but not necessary condition for incompressibility. I didn't even think to check Karamcheti, which was also sitting right in front of me.

I cited Batchelor specifically for a couple reasons. First, that text is often considered to be sort of the Bible of fluid mechanics, and it is certainly a lot more mathematically rigorous than most. Second, Batchelor formally defines incompressibility how you have previously (and in the manner that is technically correct),
\dfrac{D\rho}{dt} = 0.
Third, he goes on to do the further analysis discussing exactly how and when that condition holds. The conditions he lays out largely indicate that constant density and the above criteria are the same, if not strictly. As such, my conclusion at the end was perhaps a little bit overbroad given the fact that there are a relatively small subset of flows that do have variable density but adhere to the above.

I agree that no one simulates things like flames or variable-density mixing with the fully-compressible Navier-Stokes equations and I am pretty sure I never claimed they did, though perhaps again it was an issue of careless language. The flow, as a whole, certainly behaves much like an incompressible flow. The primary difference, as far as I am aware, is that the temperature (and/or species) is no longer decoupled from the problem, so solving the energy (and/or species) equation and an equation of state is now necessary in conjunction with mass and momentum conservation (and of course if temperature changes are large, a viscosity model like Sutherland may be necessary). This is still a fundamental difference between the variable density case and the constant density case, even when $D\rho/Dt = 0$.

I think at that point it is sort of a debate of semantics, especially since different authors have slightly different approaches. Effectively, there are three compressibility regimes: (1) one where density is constant, (2) one where density is not constant but $\nabla\cdot\vec{V}=0$ still holds, and then (3) fully-compressible flows. I think every author is pretty much in agreement that regime (1) is incompressible and regime (3) is incompressible.. Regime (2) maintains some of the features of each of the other two, however, and from my experience, it is not always treated the same in each branch of fluid mechanics. For example, I did a stint in a group that studied variable-density mixing (e.g. Rayleigh-Taylor and Richtmyer-Meshkov flows), and in all the literature in that field, regime (2) is effectively treated as its own distinct regime termed "variable-density flow" since the velocity field is incompressible but the density/temperature fields are not.

I suppose in summary, my position is this: the concept of incompressibility has several definitions that largely overlap, but whose precise definition depends on how you draw the line between compressible or incompressible flows. You can draw the line based on the velocity field, in which case variable-density flows are essentially a class of incompressible flows with variable density, or you can draw the line based on the character of the equations used to solve such flows, in which case you really sort of have three regimes instead of the two classical compressible and incompressible ones. I'd argue that, when teaching students about incompressibility for the first time, simply using "constant density" is more intuitive and effective without being incorrect if one considers there to be three compressibility regimes.

I also think it's probably a worthy discussion to have. Different factions within the fluid mechanics community treat this problem differently, and it leads to confusion, as we can see here. You've certainly got me thinking about it. I know when I teach students, I start out discussing constant density as being incompressible, and when I get to the point in the semester where I discuss the differential approach to flow analysis (as opposed to control volumes using the integral approach) I then make the distinction between constant density and zero material derivative of density.

 

[mrBart]

I am following this thread with interest. Can I rephrase boneh3ad's three regimes into bigfooted's definition as
(1) constant-density flow -> incompressible flow of an incompressible fluid
(2) variable-density flow -> incompressible flow of a compressible fluid
(3) compressible flow (nothing changes here)

Or am I talking gibberish here?

 

[boneh3ad]

I don't think that's necessarily always accurate. You can have a variable density flow with two different liquids of different densities. That would break your proposed definition.

 

[mrBart]

Ah yes, of course, I didn't consider the idea of having multiple liquids.

 

[mrBart]

I was looking for a nice reference that I could point to that shows the relationship between the velocity divergence and the criteria mentioned in Batchelor and above to make it more clear how they were derived, and the best derivation I could find was actually here on physicsforums (if somebody knows of a literature reference, please let me know):
https://www.physicsforums.com/threads/when-can-one-assume-incompressible-flow.129837/

I would also like to see such a literature reference for my thesis. Anybody?

 

[boneh3ad]

I would also like to see such a literature reference for my thesis. Anybody?

The best legitimate reference you will see is probably the Batchelor book itself. I haven't really seen anything more detailed than that.