Constraint Equations: Atwoods Machine

[sid95]

Can questions like the one given in the following pic be solved by taking the reference frame answhere in the middle of the string and not on the fixed pulley?(http://cnx.org/content/m14731/latest/pq8.gif)

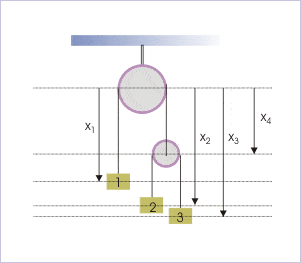
A somewhat similar method has been given in http://cnx.org/content/m14783/latest/" ( Search for Horizontal pulley system ) I'm unable to comprehend the following line:

"There is an important subtle point here. The positions of blocks are on either side of the reference point (not on the same side as usually is the case). If positive direction of reference x-direction is towards right as shown in the figure, then velocities of two blocks are : "

Why does acceleration get -ve? pl help.

 

[arildno]

I don't understand what you are meaning. Why should you make a reference frame with respect to "a middle of (some) string"??
Choice of reference frame is an arbitrary matter, but I don't see why it would help you to choose some middle of some string.

By the way, are your pulleys massless?
Do the ropes pass without friction over the pulleys, or do the pulleys rotate, with the strings not moving relative to the pulleys?

 

[sid95]

Yes the pulleys are massless, frictionless with the strings being inextinsible.

My basic question is the one given in http://cnx.org/content/m14783/latest/ ( Search for Horizontal pulley system ) wherein vB=−đxB đt . I can't understand the -ve sign.