Jesper Hellmann
- 2
- 0
Hi All
I am trying to validate a nylon (PA6 Guss) clamp which has a load of 166kN on a steel tube. I am only interested in validating the clamp.
My analytical (MatLab-Octave) calculations give me a peak Von Misses stress of about 145MPa
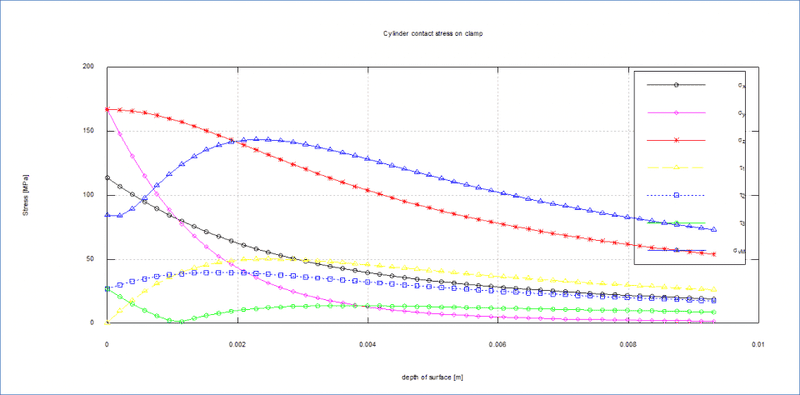
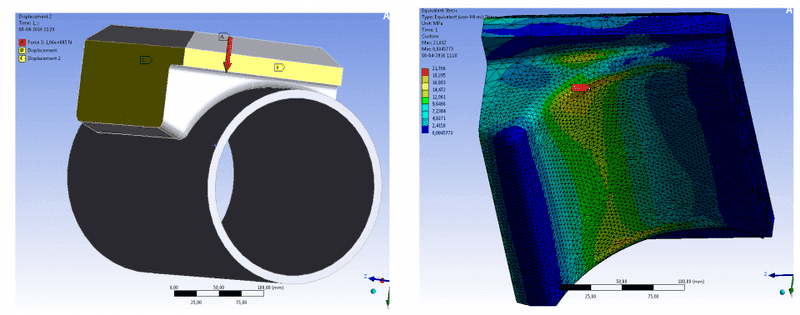
When comparing to FEM in ANSYS I only get about 30MPa
Can someone shed light on why there is such a big difference?
-Jesper Hemmlann
M.Sc. Applied Mechanics
I am trying to validate a nylon (PA6 Guss) clamp which has a load of 166kN on a steel tube. I am only interested in validating the clamp.
My analytical (MatLab-Octave) calculations give me a peak Von Misses stress of about 145MPa
When comparing to FEM in ANSYS I only get about 30MPa
Can someone shed light on why there is such a big difference?
-Jesper Hemmlann
M.Sc. Applied Mechanics