Continuous and nowhere differentiable

[saltydog]

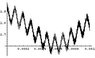
The Harvey Mudd College Math dept presents the Weierstrass' function:

f(x)=\sum_{n=0}^{\infty} B^nCos(A^n \pi x)

as an example of a continuous function nowhere differentiable if 0<B<1 and AB&gt;1+\frac{3\pi}{2}. Surely it converges to a continuous function if 0<B<1 regardless of the value of A. I base this on the Weierstrass M-test for this series.


However, I can differentiate the series leading to:

f^{&#039;}(x)=-\pi \sum_{n=0}^{\infty}(AB)^n Sin(A^n \pi x)

Doesn't this series also converge uniformly (same convergence test as above) for all x if 0<AB<1? If so, why are they requiring AB&gt;1+\frac{3\pi}{2}? I would think you could say it's nowhere differentialbe if AB>1 although greater than 1+\frac{3\pi}{2} still qualifies.

I haven't asked them, I guess I could, maybe someone here knows though.

 

[matt grime]

I suspect you half answer your own question. I would guess that the 3pi/2 thing is to force divergence of the resulting differentiated series at some point, the sin bit may be troublesome.

Tests for converegence are like that: just because we know it converges when property P is satisfied doesn't mean it diverges if P isn't satisfied - they are not usually necessary and sufficient conditions.

 

[saltydog]

Hello Matt,

I believe the function has a fractal dimension. Note the 3 attached plots of the sum of just the first five terms. The plots successively zoom-in to a small area (0,0.0001). It's self-similar and at the limit, it must have a fractal dimension although I don't know how to show this. I wish to make the following un-proven claim:

Any function with fractal dimension is differentiable nowhere.

My Analysis book includes a technique to prove another more simple "tent function" is no where differentiable and I think I'll try to attack this problem from that same perspective. I tend to think the \frac{3\pi}{2} has some specific "limiting" relevance and perhaps my analysis will uncover it. Suppose, as a last effort, I can contact Mudd but not for now.

Anyone here know how to calculate fractal dimension and can this be applied to this function?

 

[saltydog]

Alright, I'll make even a stronger claim:

A continuous function is nowhere differentialbe iff it has a fractal dimension.

Might be interesting to try and prove this . . .

 

[Hurkyl]

The line segment y = 0, 0 < x < 1 has fractal dimension 1, and it's everywhere smooth.

Back to the original question, note that you failed to consider differentiability at x = 0.

 

[saltydog]

The line segment y = 0, 0 < x < 1 has fractal dimension 1, and it's everywhere smooth.

Back to the original question, note that you failed to consider differentiability at x = 0.

Well wait a minute Hurkyl, by definition "fractal dimension" is of "non-integer" values like 1.3 or 0.98 and so fourth so I'm not sure what you mean by a straight line having a fractal dimension of 1. I'll look into your second comment.

Alright, I guess I'll dig up Mandelbrot's book . . . where is it . . . oh yea, up there, kinda dusty. But I didn't understand it back then and nothing's changed since . . .

 

[Hurkyl]

Well, I was specifically speaking about capacity dimension, one of the various things to which fractal dimension refers.

Now, fractal dimension is not, and should not, be limited to nonintegral values. For example, consider Cantor's dust. In the default construction, we replace each box with 4 copies at a scale of 1/3. If we instead use a scale of 1/4, the resulting fractal has dimension exactly 1.

 

[saltydog]

Well, I was specifically speaking about capacity dimension, one of the various things to which fractal dimension refers.

Now, fractal dimension is not, and should not, be limited to nonintegral values. For example, consider Cantor's dust. In the default construction, we replace each box with 4 copies at a scale of 1/3. If we instead use a scale of 1/4, the resulting fractal has dimension exactly 1.

Well, Cantor's dust is not continuous (and I suspect it has measure 0) and for the moment, I'd like to remain focused on continuous functions. In that regard, I have the following two questions:

1. Is Weierstrauss' curve a "fractal curve"?

2. If so, what is it's fractal dimension?

Mandelbrot, in his book which I still don't understand, states, "curves which the fractal dimension exceeds the topological dimension 1 be called "fractal curves". I believe he's referring to continuous curves.

 

[Hurkyl]

I haven't looked all that much into this subject, so I can easily have terminology wrong.

One thing I'm pretty sure you can prove is this:

If a curve C is given by a continuous, differentiable map from [0, 1], then the length of C is defined and finite. (hurray for compact sets)

So that any such curve does have Hausdorff dimension 1.

I'm pretty sure the Wierstrauss function will have infinite length, but, a curve can have infinite 1-dimensional measure (i.e. length) and still be Hausdorff dimension 1.

A curve with Hausdorff dimension greater than 1 obviously cannot be everywhere differentiable, but I would be surprised if you can get nowhere differentiability -- surely it's possible for a fractal to be differentiable at a single point, or maybe even a dense set of measure zero! (or even better, a dense set of d-dimensional measure zero, where d is the fractal dimension)


Oh, BTW, I'm pretty sure 3-dimensional fractal curves may have fractal dimension 2.

 

[saltydog]

I wish to revise my unproven claim above:

A continuous function is nowhere differentiable iff its fractal dimension exceeds 1.

Now, how do I calculate the fractal dimension of a continuous curve in the plane?

 

[Hurkyl]

Hrm... there don't seem to be any local definitions of dimension.

For example, consider this:

Let C be your favorite fractal curve with an endpoint. Then, attach a straight line segment to that endpoint. By the definitions of dimension I could find, this leaves the dimension of C unchanged, but we have clearly added a part that "ought" to be dimension 1...

(at least the line segment will have d-dimensional measure zero)

In any case, this gives you a differentiable portion.


Anyways, this proves your claim is false. Maybe your text has a definition of "local" dimension... I had taken a stab in the dark at what that might mean (meaning I tried proving something, and defined local dimension to be the thing I wanted to assume) and can prove that if f is differentiable at P, then it has dimension 1 at P, but I don't think I had anything meaningful -- I think I could prove that any continuous function had local dimension 1.


I don't know of an easy way to calculate the dimension of anything except the self-similar type of fractal, such as the Koch Snowflake. I could only suggest hammering away at the definitions.

 

[saltydog]

Thanks Hurkyl.

I've been looking at Peitgen's book on fractals and my initial efforts seem to indicate that Weierstrass' function has in fact a "self-similarity" dimension of 1. If that's the case then my proposal above is false. I'm not confident of this however. My initial reason for pursuing this line was the possibility that dimension had something to do with the \frac{3 \pi}{2} requirement. I'll spend some more time with it and if all else fails I'll e-mail the Mudd Math dept for help.

 

[saltydog]

I've since learned that the Weierstrass function is a fractal and does indeed have a fractal dimension between 1 and 2:

http://

According to this reference, for:

w(x)=\sum_{n=0}^\infty a^n Cos[2 \pi b^n x]

where:

0&lt;a&lt;1&lt;b

D_w=2+\frac{ln(a)}{ln(b)}

Note since a is less than b, the dimension is between 1 and 2.

Thus I stand by my original claim . . .

 

[Hurkyl]

Just a possibility -- maybe it will help to rewrite f as:

f(x) := \Re \sum_{n=0}^\infty b^n e^{i a^n \pi x}

 

[saltydog]

Just a possibility -- maybe it will help to rewrite f as:

f(x) := \Re \sum_{n=0}^\infty b^n e^{i a^n \pi x}

I'm sorry Hurkyl but that's just not happening for me. I realize that notation represents taking the real part of an infinite sum of complex numbers but I don't understand the relevance. Would you kindly elaborate a bit further please?

 

[Hurkyl]

Sometimes, exponentials are just easier to manipulate than trig functions -- I didn't have any particular line of attack in mind, though. This was how I planned on looking at the problem next, but I hadn't really had a chance to work on it.

 

[saltydog]

Sometimes, exponentials are just easier to manipulate than trig functions -- I didn't have any particular line of attack in mind, though. This was how I planned on looking at the problem next, but I hadn't really had a chance to work on it.

Hello Hurkly,

I've been working on it . . . very interesting. What I found especially so was the claim that functions like these are the RULE and NOT the exception! You know, like there's many more irrational numbers than rationals. Apparently same diff with "nice" functions opposed to "monster" functions. We just work with nice ones because they are ammendable to analysis. Hummm . . . another words, there's a whole world of mathematical objects out there and we only use very nearly an "infinitessimal" part of them by restricting ourselves to "differentiable" ones. Not saying you don't already know this, I didn't.

Mark Nielsen of Univ. of Idaho calls this the “Law of mathematical unapproachability”. Simply stated, “most objects in the mathematical universe are too wild for humans to describe.”

Here's the reference if anyone is interested:

Reference

And so, as those guys in philosophy over there like to talk about, I wonder what the philosophical significance of this is: we use only a small part of it to very successfully describe nature. How much better would that description be if we used a larger part!

Really, I would like to just know how to prove "nowhere differentiable". Apparently it's not as simple as just taking the derivative and showing the sum converges nowhere.

 

[Hurkyl]

Yah, that's pretty nifty, isn't it?

Actually (at least in the current context), there is a viewpoint from which one can say that everything is, in fact, describable. However, that's a far cry from, for example, being able to evaluate any real function at 0.


Anyways, back to the problem at hand... your problem is that you swapped the order of limits, an operation that isn't generally allowed. Specifically, there's a limit operation implicit in differentiating, and also with summation. So, in generally, summing then differentiating won't be the same as differentiating then summing.

 

[Data]

Well, swapping them is ok if you have uniform convergence of the differentiated series (which he does~).

ie. if

f(x) = \sum_{n=0}^\infty f_n(x)

on a closed interval I and

\sum_{n=0}^\infty f^\prime_n(x)

is uniformly convergent on I and each f^\prime_n is continuous on I then

f^\prime(x) = \sum_{n=0}^\infty f^\prime_n(x)

on I. Of course, that doesn't mean that the function isn't differentiable outside of the interval.

 

[Hurkyl]

Only when AB < 1, though. The fact the series diverges almost everywhere for AB > 1 doesn't guarantee the derivative doesn't exist.

 

[Data]

yep, that's definitely true~

 

[saltydog]

Thanks guys. I need to review some Analysis. So, as I see it I can swap the order of summation and differentiation as long as the series converges uniformly to a function which it does if AB<1. This I can prove via the Weierstrass M-test for both the function and the sum of the derivatives of f_n(x).

So, however, when AB becomes greater than 1 this no longer applies and another approach must be used. Is that correct? I found a good reference proving "a" function exists which is nowhere differentiable which is under the title of "The Weierstrass Function":

Link to proof

Think I'll get a hardcopy and spend some time going over this proof. I suspect it can be applied to prove nowhere differentiable of the cosine series above.

 

[Data]

...I can swap the order of summation and differentiation as long as the series converges uniformly...

as long as the series of derivatives converges uniformly, yes

 

[saltydog]

In an effort to approach this problem, I've chosen to fall back to an easier one first:

f(x)=\sum_{n=0}^\infty \frac{GetDistance[4^n x]}{4^n}

Where the GetDistance[x] function returns the distance from x to the integer nearest x.

This is the saw-tooth function commonly used to demonstrate continuous and nowhere differentiable. I've attached a plot superimposing f_0,f_0+f_1 andf_0+f_1+f_2. My Analysis book has a proof I can follow of it's nowhere differentiable behavior. Essentially, we seek to show:

\lim_{n\rightarrow\infty}{} \frac{f(a+h)-f(a)}{h}

does not have a limit. My interpretation of this is that it has a "corner" at all points in its domain.

Next, I'll pursue the following:

f(x)=\sum_{n=0}^\infty \frac{Sin[(n!)^2 t]}{n!}

I'm told that T.W. Koerner in his book "Fourier Analysis" gives a detailed proof that this function is nowhere differentiable. Again, this involves an analysis of the difference quotient. Apparently using the same technique, one can prove the non-differentiability of the Weierstrass function.

So, I'll work with them a bit first myself and if nothing pans out, well, it's a pleasant ride to the University library from my home.

 

[saltydog]

I've retrieved the reference cited above from T.W.Koerner's book, "Fourier Analysis". I wish to focus on reviewing the proof here of nowhere differentiable for the function below (reviewing/reporting here will help me better understand it and perhaps will help others who also wish to learn more about these functions). I'll report it in parts. I should add that he states after thoroughly investigating this proof, one should be able to apply it to prove nowhere differentiable of the cosine series of the original post which is my ultimate goal.

f(t)=\sum_{r=0}^\infty \frac{1}{r!}Sin[(r!)^2 t]

In general, we seek to investigate the difference quotient:

\mathop {\lim }\limits_{x_n \to x} \frac{f(x)-f(x_n)}{x-x_n}

In order to investigate this limit, Koerner breaks the sum into three parts which turn out to be the key to the proof:

h_n(t)=\sum_{r=0}^{n-1}\frac{1}{r!}Sin[(r!)^2 t]

k_n(t)=\frac{Sin[(n!)^2t]}{n!}

I_n(t)=\sum_{r=n+1}^{\infty}\frac{1}{r!}Sin[(r!)^2 t]

And thus:

f(t)=h_n(t)+k_n(t)+I_n(t)

These function components will be used to evaluate the difference quotient. However, some Lemmas are needed in order to set bounds on the various quantities. That's next.

 

[saltydog]

In order to prove nowhere differentiable, we must show that the difference quotient diverges at all x. Thus we seek to analyze:

\mathop {\lim }\limits_{a \to x}\frac{f(x)-f(a)}{x-a}

If we can show that for any such x, this limit increases without bound as additional elements of the function sequence are added, then we will have shown the derivative is undefined at x. It suffices therefore, to consider the absolute value of the quotient:

\mathop{\lim}\limits_{a\to x}\frac{|f(x)-f(a)|}{|x-a|}

In order to evaluate this limit, f(x) is decomposed into the three functions stated earlier which are dependent on the summation index n. Later, we will evaluate the limit as n approaches infinity. Thus we analyze:

|k_n(x)-k_n(a)|

|h_n(x)-h_n(a)|

|L_n(x)-L_n(a)|


Lemma A:

IfK\geq 3 is an integer and x\in D_f (x is in the domain of the function), then there exists an a\in <br /> <br /> D_f, such that:

\frac{\pi}{K}&lt;|x-a|\leq\frac{3\pi}{K}

and:

|Sin[Kx]-Sin[Ka]|\geq 1

This is the central idea in the whole proof and needs to be fully understood in order to proceed further.

Proof:

Consider the plot of the function Sin[Kx] and an arbitrary point, x, along it as well as the following interval I'll call I:

I=(x+\frac{\pi}{K},x+\frac{3\pi}{K}]

An attached plot shows this setup for K=6 and x=1.2.

Note that within I, Sin[Kx] takes on all values between -1 and 1. Any value, a, within this interval will be in absolute value:

\frac{\pi}{K}&lt;|x-a|\leq\frac{3\pi}{K}

But since Sin[Kx] takes on all values between -1 and 1 in this interval, I can choose a such that Sin[Ka] is either -1 or 1 so that:

|Sin[Kx]-Sin[Ka]|\geq 1

QED

Using this Lemma, we can now evaluate k_n(x) which I'll do next.

 

[saltydog]

Determination of k(n)

Using Lemma A, for any x\in D_f, we can find an "a" in the neighborhood of x such that:

\frac{\pi}{(n!)^2}&lt;|x-a|\leq\frac{3\pi}{(n!)^2}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1)

Note that as n goes to infinity, a approaches x. Thus, the final limit will be evaluated as n goes to infinity.

Using the definition of k(x) above, we have:

|k_n(x)-k_n(a)|=\frac{1}{n!}|Sin[(n!)^2 x]-Sin[(n!)^2 a]|

which, according to Lemma A is bounded from below, thus giving::

|k_n(x)-k_n(a)|\geq\frac{1}{n!}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2)

The determination of a bound for h(x) is a very interesting problem and deserves its own post:

 

[saltydog]

Analysis of h(x)

In order to analyze h_n(x), the following Lemma is needed:

Lemma B:
For all x,a\in D_f:

|Sin[x]-Sin[a]|\leq|x-a|

Proof:

Using the Mean Value Theorem we have:

Sin[x]-Sin[a]=-Cos[c](x-a)

Thus:

|Sin[x]-Sin[a]|\leq|x-a|

QED

The following is as messy as the proof gets:

Using the definition of k_n(x) above, we have:

|h_n(x)-h_n(a)|\leq\sum_{r=0}^{n-1}\frac{1}{r!}|Sin[(r!)^2x]-Sin[(r!)^2a]|

(The triangle inequality)

Using Lemma A:

\sum_{r=0}^{n-1}\frac{1}{r!}|Sin[(r!)^2x]-Sin[(r!)^2a]|\leq\sum_{r=0}^{n-1}\frac{1}{r!}|(r!)^2x-(r!)^2a|


Now:

\sum_{r=0}^{n-1}\frac{1}{r!}|(r!)^2x-(r!)^2a|=\sum_{r=0}^{n-1}(r!)|x-a|

and:

\sum_{r=0}^{n-1}(r!)|x-a|=[1+2!+3!+ . . . +(n-1)!]|x-a|

=[(n-1)!+\sum_{r=0}^{n-2}r!]|x-a|

Now:

\sum_{r=0}^{n-2}r!\leq\sum_{r=0}^{n-2}(n-2)!

Thus we have:

|h_n(x)-h_n(a)|\leq[(n-1)!+\sum_{n=0}^{n-2}(n-2)!]|x-a|

Since:

\sum_{r=0}^{n-2}(n-1)!=(n-1)(n-2)!

This reduces to:

|h_n(x)-h_n(a)|\leq 2(n-1)!|x-a|

Since:

|x-a|\leq\frac{3\pi}{(n!)^2}

Finally then:

|h_n(x)-h_n(a)|\leq\frac{6\pi}{n(n!)}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (3)

I know, this is messy but it involves a lot of good work with summations, absolute values, and inequalities. The rest is less-complicated.

 

[saltydog]

Lemma C:

\sum_{r=n}^{\infty}\frac{1}{r!}\leq\frac{2}{n!}

For n\geq 2

Proof:

\sum_{r=n}^{\infty}\frac{1}{r!}=\frac{1}{n!}+\frac{1}{(n+1)!}+\frac{1}{(n+2)!}+. . .

=\frac{1}{n!}[1+\frac{1}{n+1}+\frac{1}{(n+2)(n+1)}+\frac{1}{(n+3)(n+2)(n+1)}+. . .]

\leq\frac{1}{n!}[1+\frac{1}{2}+(\frac{1}{2})^2+(\frac{1}{2})^3+. . .]

Since the last term is a geometric series, we have:

\sum_{r=n}^{\infty}\frac{1}{r!}\leq\frac{2}{n!}

QED

Analysis of L_n(x)

Since:

|L_n(x)|\leq\sum_{r=n+1}^{\infty}\frac{1}{r!}

Using Lemma C we have:

|L_n(x)|\leq\frac{2}{(n+1)!}

Thus:

|L_n(x)-L_n(a)|\leq|L_n(x)|+|L_n(a)|\leq\frac{4}{(n+1)!}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ <br /> <br /> \ \ \ \ \ \ (4)

We now have all the expressions needed to analyze the limit of the difference quotient as n goes to infinity. I'll complete the proof next.

 

[saltydog]

Final step

We now have:

|x-a|\leq\frac{3\pi}{(n!)^2} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1)

|k_n(x)-k_n(a)|\geq\frac{1}{n!}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2)

|h_n(x)-h_n(a)|\leq\fraq{6\pi}{n(n!)}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (3)

|L_n(x)-L_n(a)|\leq\fraq{4){(n+1)!}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (4)

Recalling:

f(x)=k(x)+h(x)+L(x)

and noting that we have expressed each term in terms of n, we wish to evaluate:

\mathop{\lim}\limits_{n\to <br /> <br /> \infty}\frac{|(k_n(x)+h_n(x)+L_n(x))-(k_n(a)+h_n(a)+L_n(a))|}{|x-a|}

A short Lemma to assist with evaluating this absolute value:

Lemma D:

|a+b+c|\geq|a|-|b|-|c|

Proof:

|a|=|(a+b+c)-(b+c)|\leq|a+b+c|+|b+c|

|a|-|b+c|\leq|a+b+c|

Since:

|b+c|\leq|b|+|c|

we have:

|a|-|b|-|c|\leq|a|-|b+c|\leq|a+b+c|

QED

Thus:

|f(x)-f(a)|\geq|k_n(x)-k_n(a)|-|h_n(x)-h_n(a)|-|L_n(x)-L_n(a)|

\ \ \ \ \ \ \geq\frac{1}{n!}-\frac{6\pi}{n(n!)}-\frac{4}{(n+1)!}

Since:

\frac{1}{n!}-\frac{6\pi}{n(n!)}-\frac{4}{(n+1)!}=\frac{1}{n!}(1-\frac{6\pi}{n}-\frac{4}{n+1})

And:

\frac{1}{n!}(1-\frac{6\pi}{n}-\frac{4}{n+1})\geq\frac{1}{n!}(1-\frac{30}{n!})

Finally, for n>60,

\frac{1}{n!}(1-\frac{30}{n!})\geq\frac{1}{2(n!)}

Substituting this expression and the results from equation (1) above,

\mathop{\lim}\limits_{n\to\infty}\frac{|(k_n(x)+h_n(x)+L_n(x))-(k_n(a)+h_n(a)+L_n(a))|}{|x-a|}\geq\frac{\frac{1}{2(n!)}}{\frac{3\pi}{(n!)^2}}=\frac{n!}{6\pi}

Thus for n\geq 60, the limit goes to infinity proving that the derivative does not exist for arbitrary point x in the domain.

QED

Initially, I was overwhelmed with this proof and was having a difficult time. The author made an interesting point:

"reflection and the passage of time will help a great deal".

He was right. Now I understand it fully and am comfortable with its construction.

It's now a relatively simple matter to prove the same for the Cosine series which I'll do in a brief summary report next time.

 

[saltydog]

"relatively simple matter"

. . . . . . yea, right . . . . . I'm wrong and I ain't proud. Can someone show me how to prove:

f(x)=\sum_{r=0}^{\infty} A^r Sin[B^r x]

Is nowhere differentiable. Even with all I did above I can't apply it to this equation with A<1 and B an integer: I end up getting the difference quotient is larger than minus infinity which is meaningless.

 

[saltydog]

I was incorrectly interpreting the partial sums of a geometric series. It should be:


\sum_{r=0}^{n-1}(\frac{1}{A})^r+(\frac{1}{A})^n+\sum_{r=n+1}^{\infty}(\frac{1}{A})^r=


\frac{1-(\frac{1}{A})^n}{1-\frac{1}{A}}+(\frac{1}{A})^n+\frac{(\frac{1}{A})^{n+1}}{1-\frac{1}{A}}


The important point is to devise sizes for A and B such that the following partial differences are less than 1. The most difficult is for h_n(x). I rationalized that since factorials squared were being used above, then I should try to make the B term quite large with respect to A. In the following example, I used B=A^2.

|k_n(x)-k_n(x_0)|\geq(\frac{1}{A})^n

|I_n(x)-I_n(x_0)|\leq\frac{2}{A-1}(\frac{1}{A})^n

|h_n(x)-h_n(x_0)|\leq(\frac{A^n-1}{A-1})\frac{3\pi}{A^nA^n}

Plugging this into the differential difference quotient leads to the following expression:


\mathop{\lim}\limits_{n\to\infty}\frac{(\frac{1}{A})^n[1-\frac{2}{a-1}-\frac{3\pi(A^n-1)}{A^n(A-1)}]}{\frac{3\pi}{B^n}}

With B=A^2

This limit tends to infinity if A\geq 13

Thus,

f(x)=\sum_{r=0}^\infty(\frac{1}{13})^r Sin[(13)^{2r}x]

is nowhere differentiable.

(this is not a proof)