Contour integral with a pole on contour - justification?

[MayCaesar]

Hi everyone.

While solving different contour integrals, I stumbled upon quite a few line integrals with pole(s) on contour. I've always solved them the same way, using the rule that for such lines the integrals equal
$$\int\limits_\gamma f(z)dz=\pi i\sum\limits_n Res(f,p_n),$$
where $p_n$ are the poles, that is half the contour integral around all the poles.

In my homework (I am a PhD student), I encountered the following integral:
$$\int\limits_{-\infty}^{\infty}\frac{\cos(bx)-\cos(ax)}{x^2}dx.$$
I am using the following contour to calculate it:

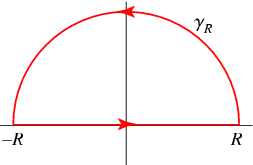
It is a very easy integral to calculate if I just use the mentioned rule. First, I write it down as follows:
$$PV\int\limits_{-\infty}^{\infty}\frac{e^{ibx}-e^{iax}}{x^2}dx,$$
where I am using the fact that $\sin(x)$ is an odd function, and the integral is taken as a principal value. It is easy to prove that in the limit of $R\to \infty$ the semi-circle integral vanishes and so we can say that our integral is simply $\pi i$ times the residue at 0. The result matches the provided answer in the book.

The problem, however, is that on the lectures, the above mentioned rule has never been introduced (neither has VP, truth said, but I think it does not need an introduction in this context). As such, I feel that I need to provide, at least, some informal proof of it. Our professor doesn't require us to do all formal math, but she does expect us to, at least, verbally explain what we did and why.

No matter how hard I tried, I haven't managed to come up with any reasonable "intuitive" explanation. Extensive search in the Internet hasn't yielded anything either. The only theorem I found that was any close to what I need is Plemelj theorem, but I don't think I can prove it myself, and also the proof will probably be too complex for such a simple problem. Also I know that there is some theorem I encountered a couple of years ago that said something about functions defined at points of non-continuity as
$$f(x_0)=\frac{1}{2}(\lim\limits_{x\to x_0-0}f(x)+\lim\limits_{x\to x_0+0}f(x)),$$
which could be used in this case as I take the limit of the bottom line of the contour to the x-axis from above and from below it. But I haven't found the exact formulation of it.

Could someone please link something relevant to me that would help me justify this formal rule of integration? Ideally I would like to justify it universally, for all integrals, although a justification for this particular integral would also be helpful. Thanks!

 

[ShayanJ]

I remember myself looking for a similar thing and finding nothing nowhere. Till I started thinking on it myself!
The answer lies in the proof of Cauchy's integral formula. There, at one point an integration around the pole is done which is on a full circle centered around the pole and that is how the $2\pi$ shows up. Just go back there and try to prove it with a contour which traverses a smaller angular interval and you will see there will be no problem and any other angle can easily show up instead of $2\pi$(of course depending on the contour).

 

[MayCaesar]

Thank you so much! After looking up the Cauchi's formula proof and doing some search in the Internet, I came across a very nice tiny lemma proven by one of the posters at StackExchange:

http://math.stackexchange.com/quest...ral-calculation-with-0-pole-and/184874#184874

Unfortunately, it works only for the limit of a zero radius circle, and also it doesn't seem to work for poles of higher orders than 1st, but I think I saw a mention somewhere that the method of calculation I described above didn't work for higher orders anyway.
So we can calculate the integral in question the following way. We can take a large arc as shown on the picture and a very small arc, plus the real axis lines, so the pole is out of the figure's surface. Total contour integral is then 0, small arc integral is $-\pi i Res_0 f(z)$ (the sign is minus since we go clockwise), large arc integral vanishes at infinite radius, and so we have for the integral $I$: $I-\pi i Res_0 f(z)=0$.

Actually, now that I've seen this lemma's proof, I understand where Cauchi's integral formula comes naturally from. For small circles, the holomorphic function values close to the pole of the 1st order are about the same as at it (just like any continuous function varies little on small ranges in real space), so contour integral will just equal the angular length of the arc we are integrating over times the value ($i$ comes from differentiating $e^{i\theta]}$ over $\theta$. For larger circles, this is not necessarily the case, however, for the special case of $2\pi$ angle we still get this formula regardless of the radius since "normal" complex functions are periodic over angle (and for "non-normal" functions like logarithm or root residue theorem doesn't work anyway).

This all finally starts making sense to me. I've always wondered how Cauchi's formula could work for nearly any complex function, but now I understand that this all comes from angular periodicity and properties of holomorphic functions.