- #1
ManDay
- 159
- 1
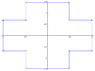
The Schwarz-Christoffel mapping (a Riemann-mapping) from the unit disk (z-plane) to a twice-symmtric area (a cross, ζ-plane)
$$ \zeta : \mathbf C \to \mathbf C $$
is given by:
$$\frac{ \mathrm{d}\zeta }{ \mathrm{d} z} = \left( \frac{ ( z^2-b^2 ) ( z^2-\frac 1 {b^2} ) }{ ( z^2-a^2 ) ( z^2-\frac 1 {a^2} ) ( z^2-c^2 ) ( z^2-\frac 1 {c^2} ) } \right)^\frac12 $$
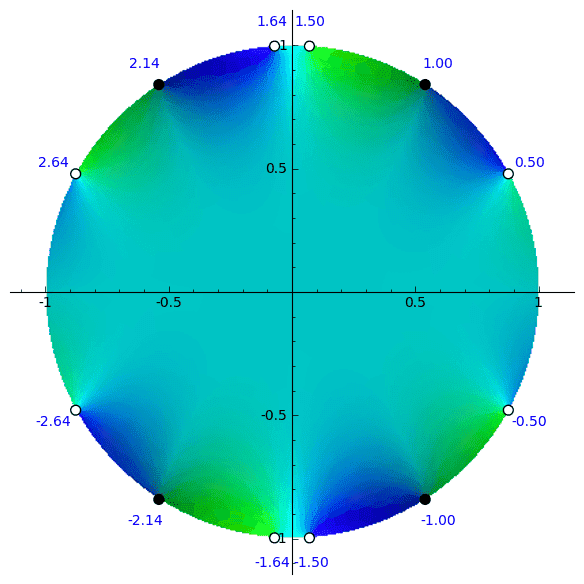
where a, b, and c are points in counter-clockwise order in the first quadrant on the unit circle. If the integration constant is chosen such that
$$\zeta ( z ) = \int_0^z \mathrm{d}y \frac{ \mathrm{d}\zeta }{ \mathrm{d} y}(y)$$
the cross-shape in the ζ-plane to which the unit circle in the z-plane is mapped has a symmetry about the real and the imaginary axis, i.e. ∀ |z| = 1:
$$ \zeta \left( \frac 1 z \right) = \bar \zeta ( z ) $$
$$ \zeta \left( - \frac 1 z \right) = -\bar \zeta ( z ) $$
This is true and evident from numeric evaluation but it is contradicted by:
$$ \zeta \left( \frac 1 z \right) = \int_0^1 \mathrm{d}y \frac{ \mathrm{d}\zeta }{ \mathrm{d} y}(y) + \int_1^{\frac 1 z }\mathrm{d}y \frac{ \mathrm{d}\zeta }{ \mathrm{d} y}(y) $$
Transformation of the second integral with x := 1/y
$$\begin{aligned}\int_1^{\frac 1 z }\mathrm{d}y \frac{ \mathrm{d}\zeta }{ \mathrm{d} y}(y) &= -\int_1^z \mathrm{d}x \frac 1 {x^2} \frac{ \mathrm{d}\zeta }{ \mathrm{d} y}\left(y = \frac 1 x \right) \\
&= -\int_1^z \mathrm{d}x \frac{ \mathrm{d}\zeta }{ \mathrm{d} x} ( x )
\end{aligned}$$
Where the second line follows from the first by simply inserting dζ/dz and distributing the x² factor on the fraction and pulling out pairwise terms of the forms b and 1/b. So we have
$$ \zeta \left( \frac 1 z \right) = \int_0^1 \mathrm{d}y \frac{ \mathrm{d}\zeta }{ \mathrm{d} y}(y) - \int_1^z\mathrm{d}y \frac{ \mathrm{d}\zeta }{ \mathrm{d} y}(y) $$
but ∫01… is purely real and ∫1z… is mixed real and imaginary, so this contradicts the symmetry about the real axis from above because
$$ \zeta ( z ) = \int_0^1 \mathrm{d}y \frac{ \mathrm{d}\zeta }{ \mathrm{d} y}(y) + \int_1^z\mathrm{d}y \frac{ \mathrm{d}\zeta }{ \mathrm{d} y}(y) $$
In fact, the transformation turns out to be wrong. ∫11/z… is indeed the complex conjucate of ∫1z…, not the negative, so there must be a problem with the derivation above.
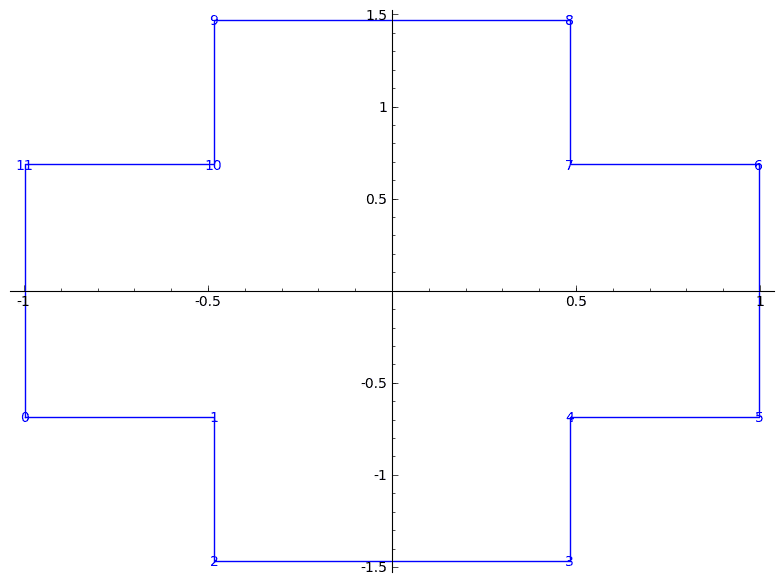
Note: The cross in the ζ-plane is mapped such that 0 maps to the center, 1 maps to the tip of the left arm (i.e. negative real part, 0 imaginary part), -1 maps to the tip of the right arm and i, -i respectively, map to tips of the bottom and top arm. Therefore ∫01… points from the center outwards to the left arm and is purealy real while, say, ∫1i… points from the tip of the left arm to the tip of the bottom arm and is mixed real and imaginary.
PS: I'm afraid this is again related to choosing the correct branches on the exponentiation in the integral, so that by the (correct) choice of branches, I get the correct result, that is, the complex conjucate. But this seems messed up: Is there a tool which allows me to treat the transformation consistently without thinking through in detail which branch goes where and when so these be equivalent?
PS II: Even despite that vague suspicion, I can't really see how choosing branches could yield the complex conjugate, because that would only yield a sign for the expression (unless I switch branches inside the interval)
PS III: I'm aware of alternative methods to prove the relation, but that doesn't explain the above contradiction.
$$ \zeta : \mathbf C \to \mathbf C $$
is given by:
$$\frac{ \mathrm{d}\zeta }{ \mathrm{d} z} = \left( \frac{ ( z^2-b^2 ) ( z^2-\frac 1 {b^2} ) }{ ( z^2-a^2 ) ( z^2-\frac 1 {a^2} ) ( z^2-c^2 ) ( z^2-\frac 1 {c^2} ) } \right)^\frac12 $$
where a, b, and c are points in counter-clockwise order in the first quadrant on the unit circle. If the integration constant is chosen such that
$$\zeta ( z ) = \int_0^z \mathrm{d}y \frac{ \mathrm{d}\zeta }{ \mathrm{d} y}(y)$$
the cross-shape in the ζ-plane to which the unit circle in the z-plane is mapped has a symmetry about the real and the imaginary axis, i.e. ∀ |z| = 1:
$$ \zeta \left( \frac 1 z \right) = \bar \zeta ( z ) $$
$$ \zeta \left( - \frac 1 z \right) = -\bar \zeta ( z ) $$
This is true and evident from numeric evaluation but it is contradicted by:
$$ \zeta \left( \frac 1 z \right) = \int_0^1 \mathrm{d}y \frac{ \mathrm{d}\zeta }{ \mathrm{d} y}(y) + \int_1^{\frac 1 z }\mathrm{d}y \frac{ \mathrm{d}\zeta }{ \mathrm{d} y}(y) $$
Transformation of the second integral with x := 1/y
$$\begin{aligned}\int_1^{\frac 1 z }\mathrm{d}y \frac{ \mathrm{d}\zeta }{ \mathrm{d} y}(y) &= -\int_1^z \mathrm{d}x \frac 1 {x^2} \frac{ \mathrm{d}\zeta }{ \mathrm{d} y}\left(y = \frac 1 x \right) \\
&= -\int_1^z \mathrm{d}x \frac{ \mathrm{d}\zeta }{ \mathrm{d} x} ( x )
\end{aligned}$$
Where the second line follows from the first by simply inserting dζ/dz and distributing the x² factor on the fraction and pulling out pairwise terms of the forms b and 1/b. So we have
$$ \zeta \left( \frac 1 z \right) = \int_0^1 \mathrm{d}y \frac{ \mathrm{d}\zeta }{ \mathrm{d} y}(y) - \int_1^z\mathrm{d}y \frac{ \mathrm{d}\zeta }{ \mathrm{d} y}(y) $$
but ∫01… is purely real and ∫1z… is mixed real and imaginary, so this contradicts the symmetry about the real axis from above because
$$ \zeta ( z ) = \int_0^1 \mathrm{d}y \frac{ \mathrm{d}\zeta }{ \mathrm{d} y}(y) + \int_1^z\mathrm{d}y \frac{ \mathrm{d}\zeta }{ \mathrm{d} y}(y) $$
In fact, the transformation turns out to be wrong. ∫11/z… is indeed the complex conjucate of ∫1z…, not the negative, so there must be a problem with the derivation above.
Note: The cross in the ζ-plane is mapped such that 0 maps to the center, 1 maps to the tip of the left arm (i.e. negative real part, 0 imaginary part), -1 maps to the tip of the right arm and i, -i respectively, map to tips of the bottom and top arm. Therefore ∫01… points from the center outwards to the left arm and is purealy real while, say, ∫1i… points from the tip of the left arm to the tip of the bottom arm and is mixed real and imaginary.
PS: I'm afraid this is again related to choosing the correct branches on the exponentiation in the integral, so that by the (correct) choice of branches, I get the correct result, that is, the complex conjucate. But this seems messed up: Is there a tool which allows me to treat the transformation consistently without thinking through in detail which branch goes where and when so these be equivalent?
PS II: Even despite that vague suspicion, I can't really see how choosing branches could yield the complex conjugate, because that would only yield a sign for the expression (unless I switch branches inside the interval)
PS III: I'm aware of alternative methods to prove the relation, but that doesn't explain the above contradiction.
Attachments
Last edited: