Kruidnootje
- 24
- 0
I plotted 3 points on Google Earth.
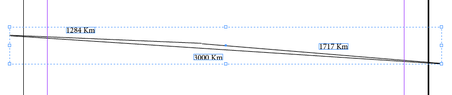
West (point A) to slightly North point (point B)= 1284 Km A-B
From Point B to further East Point (point C) = 1717 Km
Then a straight direct line from point C back to point A
The Perimeter = 6001 Km
Area = 57 491 Km
Angle A = 1.711 degrees
Angle B = 177.01 degrees
Angle C = 1.279 degrees
(sorry can't find any degree sign symbol on the right)
Problem:
When I drop a perpendicular line down from Angle B to the longest line (3000) the height is 18 Km
When I calculate by using the formula h = 57491/1500 = 38.33 Km
Is the discrepancy caused by the curvature of the Earth on Google maps? Can one even form an accurate triangular representation in this manner?
West (point A) to slightly North point (point B)= 1284 Km A-B
From Point B to further East Point (point C) = 1717 Km
Then a straight direct line from point C back to point A
The Perimeter = 6001 Km
Area = 57 491 Km
Angle A = 1.711 degrees
Angle B = 177.01 degrees
Angle C = 1.279 degrees
(sorry can't find any degree sign symbol on the right)
Problem:
When I drop a perpendicular line down from Angle B to the longest line (3000) the height is 18 Km
When I calculate by using the formula h = 57491/1500 = 38.33 Km
Is the discrepancy caused by the curvature of the Earth on Google maps? Can one even form an accurate triangular representation in this manner?