Control theory: block diagram, problem (detailed below)

[thegreengineer]

I´m taking a course on control engineering and I have a test next Tuesday so I need to study the basics which are: Laplace transform, simplification of block diagrams, and analysis of transient and steady state responses. Right now I am dealing with the second one.

I know the basic rules of block diagram simplification and the specific case I want to deal in this thread is this one:

NEGATIVE FEEDBACK LOOP

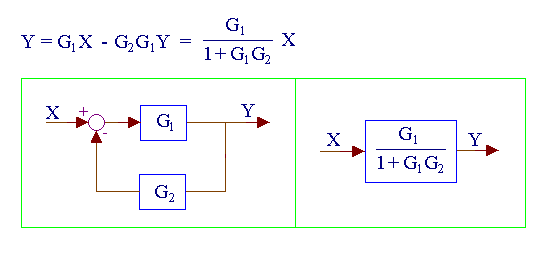
Image taken from: http://www.msubbu.in/sp/ctrl/BD-Rules.htm
In other words, the equivalent transfer function is the product of the feed-forward path divided by one plus the product of the transfer functions that make the loop.

So I get stuck on this and the problem is that the author (the book is MODERN CONTROL ENGINEERING by KATSUHIKO OGATA 5th ed.) skipped steps explaining how to simplify this:

This is the way the author simplified it:
https://scontent-lax3-1.xx.fbcdn.net/v/t1.0-9/14358649_1778386355779234_9131464410329635376_n.jpg?oh=e7cd4c25c4caafab8260b0e61c814aa2&oe=583D6FC2
The author simplified from step c) to step d). The equivalent transfer function is not similar to what I get. I'll explain you what I did and I will compare the results:

First of all let's start in step c). The blocks containing the transfer functions \frac{G_{1}G_{2}}{1-G_{1}G_{2}H_{1}} and G_{3} are in series, therefore the equivalent transfer function is \frac{G_{1}G_{2}G_{3}}{1-G_{1}G_{2}H_{1}}. The reduced diagram is the following:
https://scontent-lax3-1.xx.fbcdn.net/v/t1.0-9/14355645_1778854725732397_2673141930938132618_n.jpg?oh=187ae0673bdb279bd12d64a28207f93c&oe=5874F734
Here's now where my problem starts. As far as I see the loop formed by the second-to right summation point, the transfer function \frac{G_{1}G_{2}G_{3}}{1-G_{1}G_{2}H_{1}}, and the transfer function \frac{H_{2}}{G_{1}} are forming the negative feedback loop configuration, when I did it the result was not the same as the author's. Trust me, I actually did it and I would put the proof below but my computer is failing so don't insist please, I'm trying to understand this topic but I keep stuck so I would want someone to tell me what the author exactly did step by step.

 

[thegreengineer]

I mean, how did he actually simplify to that?

 

[Aaron Crowl]

$$Y=\frac{G_{1}G_{2}G_{3}}{1-G_{1}G_{2}H_{1}}X -
\frac{G_{1}G_{2}G_{3}}{1-G_{1}G_{2}H_{1}}\frac{H_{2}}{G_{1}}Y
$$

$$Y=\frac{\frac{G_{1}G_{2}G_{3}}{1-G_{1}G_{2}H_{1}}}{1+\frac{G_{1}G_{2}G_{3}}{1-G_{1}G_{2}H_{1}}\frac{H_{2}}{G_{1}}}X
$$

$$Y=\frac{\frac{G_{1}G_{2}G_{3}}{1-G_{1}G_{2}H_{1}}}{1+\frac{1G_{2}G_{3}}{1-G_{1}G_{2}H_{1}}\frac{H_{2}}{1}}\frac{1-G_{1}G_{2}H_{1}}{1-G_{1}G_{2}H_{1}}X
$$

$$Y=\frac{\frac{G_{1}G_{2}G_{3}}{1}}{1-G_{1}G_{2}H_{1}+\frac{1G_{2}G_{3}}{1}\frac{H_{2}}{1}}X
$$

You probably just mixed up a numerator and denominator somewhere

edit: Earlier I had a '+' instead of '-' in that first equation. Fixed!

 

[thegreengineer]

Please someone answer. I have an exam of this on Tuesday. Please, I'm desperate.

I find this example everywhere and everyone skips the same damn steps. Please, I'm tired of getting stuck and confused. I did this following the definition of negative feedback, and I got the result I am showing in the photo which is completely different, and my teacher will just give us thirty minutes for the exam and I can't waste too much time with long steps.

Please I need help. If I can't even do this simple problem, who thinks I'm going to do harder problems?

https://scontent-lax3-1.xx.fbcdn.net/v/t1.0-9/14368868_1779167525701117_2312698362951297674_n.jpg?oh=166ebb913302a2f873efc60a6c857bb5&oe=58811457

 

[Aaron Crowl]

Take a deep breath. This part that you did was unnecessary.

$$Y=\frac{\frac{G_{1}G_{2}G_{3}}{1-G_{1}G_{2}H_{1}}}{1+\frac{G_{1}G_{2}G_{3}}{1-G_{1}G_{2}H_{1}}\frac{H_{2}}{G_{1}}}X=\frac{\frac{G_{1}G_{2}G_{3}}{1-G_{1}G_{2}H_{1}}}{1+\frac{G_{1}G_{2}G_{3}H_{2}}{G_{1}^2-G_{1}G_{2}H_{1}}}X$$

It's easier to simply eliminate the term $\frac{1}{1-G_{1}G_{2}H_{1}}$ from the numerator and denominator like so:

$$Y=\frac{\frac{G_{1}G_{2}G_{3}}{1-G_{1}G_{2}H_{1}}}{1+\frac{G_{1}G_{2}G_{3}}{1-G_{1}G_{2}H_{1}}\frac{H_{2}}{G_{1}}}X=\frac{\frac{G_{1}G_{2}G_{3}}{1-G_{1}G_{2}H_{1}}}{1+\frac{1G_{2}G_{3}}{1-G_{1}G_{2}H_{1}}\frac{H_{2}}{1}}\frac{1-G_{1}G_{2}H_{1}}{1-G_{1}G_{2}H_{1}}X=\frac{G_{1}G_{2}G_{3}}{1-G_{1}G_{2}H_{1}+1G_{2}G_{3}H_{2}}X$$

Does that make it more clear?