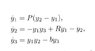Convection described by Lorenz's Equation Bifurcation

[hanson]

Hi all!
I am currently reading the text "Practical Bifurcation and Stability Analysis" by Seyedel for an introduction to practical bifurcation theory.
I do not tatolly understand the theory and hope that some of you could help explain to an idiot like me.

I have read till P.80 of the books (I scanned a few pages, see below please).

I would like to ask, in the bifurcation diagram, there is a hopf bifurcation at R=33.45. My intuition is that, there are periodic oscialltions from R=29 to 33.45, is it correct? But why would there be period obits at R=22.3, R=19 as given by below diagrams?

I thought that at R=22.3 or 19, there are just stable and unstabl equilibria as indicated in the bifurcation diagram, why would there be periodic orbits?

I am sure that something is wrong with my concepts, please kindly rectify me.

 

[HallsofIvy]

Stable and unstable equilibria will not result in Hopf bifurcation. You have to have periodic orbits of "cascading" periods in order to have that kind of chaotic bifurcation.

 

[hanson]

Isn't a hopf birfurcation a birfurcation from a branch of equilibria to a branch of periodic oscillations? (periodoic oscillations = periodic orbits = closed trajectories?)

 

[hanson]

I jstu interpret the bifurcatio diagram as follows:

For R<29, there are only stable and unstable equilibria, no periodic orbits since the hopf bifurcation value is not reached yet.

The hopf bifurcation exist when R=33.45 where periodoic orbits are born but STOP AT R=29? (I know it is wrong...but what does the shaded area means?)

Or it means for R<33.45, period orbits are born? That means there are periodoic orbits where all values of R on the left of the hopf bifurcation value? But why the curved dashed curve end around R= 29? I just don't get it...

Please kindly help.

 

[J77]

Steady states undergo Hopf bifurcations; steady states on the bifurcating branch then have an extra pair of complex conjugate eiegnvalues in the right-half of their stability plane.

A branch of periodic solutions emanate from a Hopf bifurcation.

Stable and unstable equilibria will not result in Hopf bifurcation. You have to have periodic orbits of "cascading" periods in order to have that kind of chaotic bifurcation.

Equilibria (staedy states) undergo Hopf bifurcations. The periodic orbit which emanates from this point may undergo a period-doubling cascade to chaos - though there are other routes

In your second thumbnail, you have a subcritical Hopf bifurcation (criticality can be determined from the Jacobian or higher order terms of normal form in more complex systems). This results in an unstable periodic solution growing in the "backward" direction. Your steady state was initially stable (solid line) but becomes unstable after the bifurcaiton (dashed line).

Fig.2.32 presumably shows this unstable periodic solution.

In your last thumbnail, I don't have Seydel on me so can't look it up, but is that the branch of periodic solutions (shown in dots) cutting back on itself. In this figure, I don't think they indicate stability - 1. the steady state is shown as solid after the bifurcation (if it is steady state); 2. After such a cut-back, of periodic solutions emanating from a Hopf bifurcation, you would expect the periodic solutions to undergo a saddle-node bifurcation of limit cycles and achieve stability, of which I see no indication.

Through in more details if you want - we don't get many bifurcation questions on here, well not enough!