Convergence of Series: Homework Statement and Attempt at Solution

[ptolema]

it's a new semester, and we're at it again. series abounds!

Homework Statement

Let

.
Determine whether the following series converges:

Homework Equations

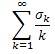
-1 $$\leq$$ $$\sigma$$_k $$\leq$$ 1

The Attempt at a Solution

i feel like the series inherently diverges because of the 1/k element. also,

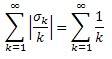, so i know that the series does not converge absolutely. of course, that isn't solid proof that the series diverges, but other convergence tests are harder to work with for this particular problem. since the $$\sigma$$_k and 1/k series both diverge, it makes sense to me that the above series would also diverge. could someone help me make this less intuitive and find a more direct approach?

 

[Dick]

Think about doing some algebra on -1/(3*k)+1/(3*k+1)+1/(3*k+2). Does that help you get past intuition?

 

[ptolema]

after a bit of algebra, I got to

. I tried taking the limit as k-->infinity, and the limit turned out to be zero. from this, i can kind of tell that as k increases, the sums of consecutive terms in the series get smaller and approach zero. this suggests convergence.
also, after looking at it for a while, I decided to treat it as a weird case of alternating series. since lim 1/k as k->infinity is zero, i reached the tentative conclusion that the series converges. as any of my arguments valid?

 

[Dick]

after a bit of algebra, I got to

. I tried taking the limit as k-->infinity, and the limit turned out to be zero. from this, i can kind of tell that as k increases, the sums of consecutive terms in the series get smaller and approach zero. this suggests convergence.
also, after looking at it for a while, I decided to treat it as a weird case of alternating series. since lim 1/k as k->infinity is zero, i reached the tentative conclusion that the series converges. as any of my arguments valid?

It's DEFINITELY not convergent. Look at the expression you got. For large k that's approximately 9k^2/(27k^3) (ignoring smaller powers). That's 3/k. You have to add those up for all k. It's like a harmonic series. To formalize it think about a limit comparison test.

 

[Gib Z]

We can save ourselves some algebra and a limit comparison test. Firstly, we can ignore the first term of the series since it won't effect convergence. Call this adjusted series S. Then note the consecutive pairs $$\frac{1}{3k+2}, \frac{-1}{3(k+1) }$$ will "telescope", leaving a small positive residue term each time. Then $$S > \sum_{k=1}^{\infty} \frac{1}{3k+1} > \sum_{k=1}^{\infty} \frac{1}{3(k+1)} = \frac{1}{3} \sum_{k=2}^{\infty} \frac{1}{k}$$ .