- #1
ptolema
- 83
- 0
it's a new semester, and we're at it again. series abounds!
Let
 .
.
Determine whether the following series converges:
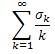
-1 [tex]\leq[/tex] [tex]\sigma[/tex]k [tex]\leq[/tex] 1
i feel like the series inherently diverges because of the 1/k element. also,
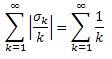 , so i know that the series does not converge absolutely. of course, that isn't solid proof that the series diverges, but other convergence tests are harder to work with for this particular problem. since the [tex]\sigma[/tex]k and 1/k series both diverge, it makes sense to me that the above series would also diverge. could someone help me make this less intuitive and find a more direct approach?
, so i know that the series does not converge absolutely. of course, that isn't solid proof that the series diverges, but other convergence tests are harder to work with for this particular problem. since the [tex]\sigma[/tex]k and 1/k series both diverge, it makes sense to me that the above series would also diverge. could someone help me make this less intuitive and find a more direct approach?
Homework Statement
Let
Determine whether the following series converges:
Homework Equations
-1 [tex]\leq[/tex] [tex]\sigma[/tex]k [tex]\leq[/tex] 1
The Attempt at a Solution
i feel like the series inherently diverges because of the 1/k element. also,