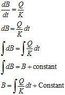zealous131
- 4
- 0
Hi,
I need to ask a very basic question and am very weak at calculus. I have an equation d(B)/dt=Q/K. Where K is a constant and Q is a function of time. B is the variable, which when differentiated w.r.t. time gives the Q. I want to convert this equation into integral form. Can anyone help me out on this? I will really really appreciate any help! Thanks!
I need to ask a very basic question and am very weak at calculus. I have an equation d(B)/dt=Q/K. Where K is a constant and Q is a function of time. B is the variable, which when differentiated w.r.t. time gives the Q. I want to convert this equation into integral form. Can anyone help me out on this? I will really really appreciate any help! Thanks!