Crate lowered by two ropes and deceleration at each point of contact with rope

[Pipsqueakalchemist]

Homework Statement

Question and attempts below

Relevant Equations

Newton’s law
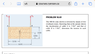
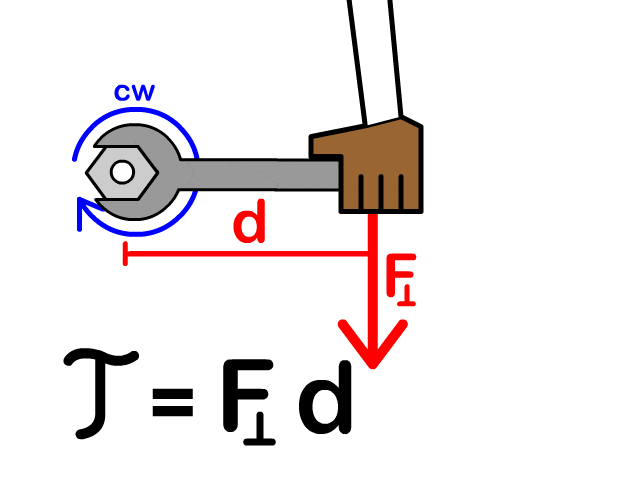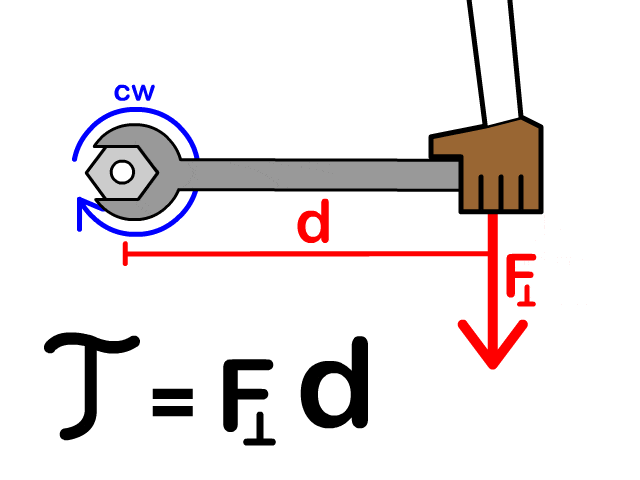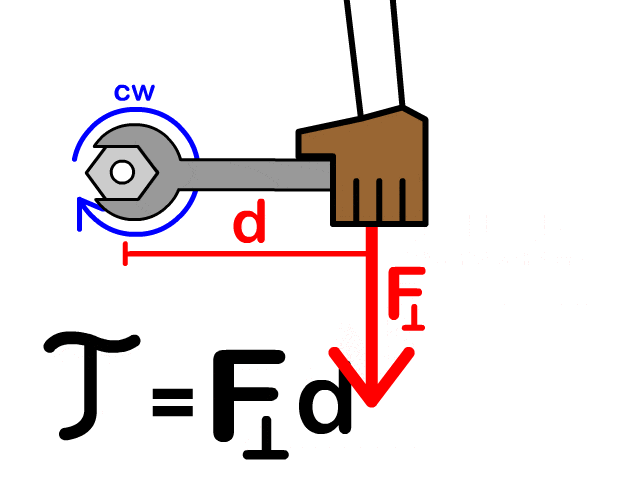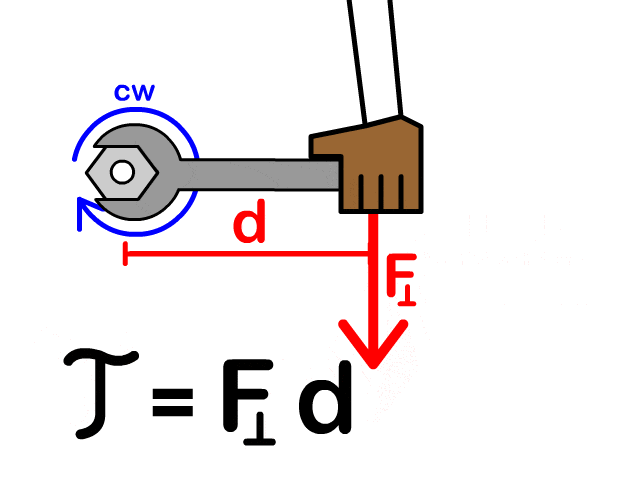
Relative acceleration

For this question, I don’t understand the steps for the relative motion part. When I try it I get angular acceleration to be zero which is obviously wrong. The solution doesn’t consider the Y distance between G and A but I don’t understand why. In the relative motion equation it’s suppose to be the position vector from G to A but if you consider that like I did it’s wrong. This is how I’ve been solving the problems so far and in rigid body kinematic so I’m very confused right now

 

[BvU]

Homework Statement:: Question and attempts below
... I’m very confused right now

Sometimes it helps to type out the problem statement

When I try it I get angular velocity to be zero which is obviously wrong

This isn't about angular velocity, but about angular acceleration

And I agree with

PS You should try to learn latex

There's a good tutorial on LaTeX here.

$\$

 

[Pipsqueakalchemist]

Sorry I meant angular acceleration

 

[Pipsqueakalchemist]

So did I do something wrong and I’m not suppose to consider the Y component of the position vector from G to A?

 

[Pipsqueakalchemist]

Anyone?

 

[Lnewqban]

... The solution doesn’t consider the Y distance between G and A but I don’t understand why.

The only forces inducing a moment or torque that induces the angular acceleration are all vertical.
The relative distances to be considered for calculating that torque should be all perpendicular to those forces; therefore, horizontal distances between fulcrums and projection of vertical forces are the only significant in this problem.

 

[Pipsqueakalchemist]

The only forces inducing a moment or torque that induces the angular acceleration are all vertical.
The relative distances to be considered for calculating that torque should be all perpendicular to those forces; therefore, horizontal distances between fulcrums and projection of vertical forces are the only significant in this problem.

But I’m using relative acceleration so there’s no moments or torques in the equation.

 

[Pipsqueakalchemist]

Is it safe to say that when using two point on an rigid body whose velocity are parallel to each other that we only consider perpendicular distance? Bc I don’t think I’ve had an problem where the two points being parallel to each other so I always consider both horizontal and vertical distances.

 

[Lnewqban]

But I’m using relative acceleration so there’s no moments or torques in the equation.

What is the reason for the angular acceleration about G then?
TA>TB because the brake of crane A is applied more strongly than the brake of crane B.

Wherever there is a mass under acceleration (positive or negative) there is a force.
There is no force without direction and intensity.

In this case, the upward braking forces applied at A and B are different in magnitude, so one side of the crate vertically deccelerates more than the other and its center of mass vertically deccelerates at a rate between those two, and at the same time it angularly accelerates because the unbalanced pair of vertical braking forces applied 3.3 feet on its left and 3.3 feet on its right side.
Hence, the member 3.3xalpha in the solution equations (3) and (4) of the book.

 

[Pipsqueakalchemist]

What is the reason for the angular acceleration about G then?
TA>TB because the brake of crane A is applied more strongly than the brake of crane B.

Wherever there is a mass under acceleration (positive or negative) there is a force.
There is no force without direction and intensity.

In this case, the upward braking forces applied at A and B are different in magnitude, so one side of the crate vertically deccelerates more than the other and its center of mass vertically deccelerates at a rate between those two, and at the same time it angularly accelerates because the unbalanced pair of vertical braking forces applied 3.3 feet on its left and 3.3 feet on its right side.
Hence, the member 3.3xalpha in the solution equations (3) and (4) of the book.

So is it the case that since all the acceleration are parallel I can just focus on the perpendicular distances. Bc as I said above I’ve always considered both the horizontal and vertical distances when considering the position vector (r_AB) and I’ve noticed in these scenarios A and B had acceleration, velocity that weren’t parallel