confusedatmath
- 14
- 0
View attachment 1901
View attachment 1902
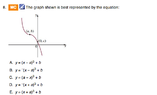
I am confused about using horizontal transformations such as
f(x+a) and f(x-a) to interpret these graphs.
View attachment 1902
I am confused about using horizontal transformations such as
f(x+a) and f(x-a) to interpret these graphs.