kamil.borkowski
- 8
- 0
Hi there!
I have a problem to find an equation of r(t), which will help me to describe motion of blue dot. I have seen many cases where there is a linear motion and you can write φ=ωt , r=V0t, but here there is an acceleration. I think I can write φ=εt2/2, but what about r(t) ? I have tried differencial equation
r = at2/2 + r0 → r = (r''-rφ')t2/2 + r0, but not sure if it's right. I need all this to have equation of path r(φ). r0 is initial position of blue dot, where V0=0 and ω=0. Cheers!
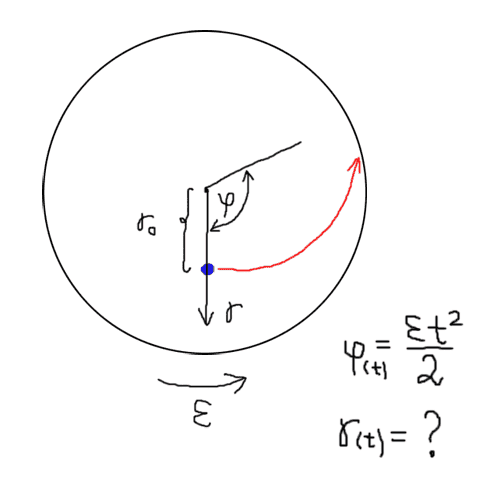
I have a problem to find an equation of r(t), which will help me to describe motion of blue dot. I have seen many cases where there is a linear motion and you can write φ=ωt , r=V0t, but here there is an acceleration. I think I can write φ=εt2/2, but what about r(t) ? I have tried differencial equation
r = at2/2 + r0 → r = (r''-rφ')t2/2 + r0, but not sure if it's right. I need all this to have equation of path r(φ). r0 is initial position of blue dot, where V0=0 and ω=0. Cheers!
Last edited: