Curvilinear n&t motion question engineering mechanics

[Kasthuri]

Homework Statement

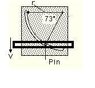
A pin is constrained to move in a circular slot of radius 39mm. At the same time a slotted bar also constrains the pin to move down with constant velocity 8mm/s. (as shown in attached diagram).

What is the magnitude of the acceleration of the pin for the position shown?

Homework Equations

NB: instead of using n&t as hinted as suggested, I used x and y coordinate system

The Attempt at a Solution

time taken for pin to move to position:

[39mm x sin(73)] / 8 mm/s = 4.6619... seconds

position of pin is:

x = 39 - sqrt(39^2 - 8^2*t^2)
so
x = 39 - sqrt(1521 - 64t^2)
y = -8t

pin's velocity is downward hence, it's acceleration is due to sideways movement: (x direction):

x^2 - 2*39*x = -64t^2 **

taking differential of **:
2*x*dx/dt - 2*39*dx/dt = -128t ***taking differential of ***:
2*dx/dt + 2x*d^2x/dt^2 - 2*39*d^2x/dt^2 = -128 ****

Now, substitute t=4.6613.. into ** to get x = 17.83... mm

then substitute x and t values into *** to get dx/dt = 14.0959... mm/s

then substitute dx/dt into **** to get d^2x/dt^2 = 2.05515...mm/s^2therefore,

answer: 2.055185 mm/s^2

However, my answer is wrong and I have no idea why?

thank you for any help you can give me

 

[oli4]

Hi kasthuri, I don't know if I could help you but you apparently forgot to actually attach the "attached diagram" :)
side question: are you familiar with the lagrangian formalism ?

 

[Kasthuri]

Sorry and thanks for telling me! I've attached it on my reply
Also, I don't know about the lagrangian formalism.
:)

 

[oli4]

Hi, Katsthuri, sorry for my silly question about the lagrangian, I thought you were resolving a different kind of problem and I didn't read your whole post to well since the picture wasn't available
your (**) is wrong, first.
if you are just going to look for derivatives it could not matter too much, but apparently later you use it to find x at the given instant.
I don't follow well you derivations, but one thing is sure, you found the wrong x.
You have correctly expressed x as a function of t
x=39-√(1521-64t²)
you know the position is at t=4.6619, if you plug t there, you won't get x=17.83 but x=11.4, so there you have your first problem.
Now, since you have x(t), why don't you just derive it twice to have the x acceleration as a function of t and then plug in 4.6619 ?

Cheers...