OneMoreName
- 10
- 1
Hi there,
This is a problem concerning hyperbolic type partial differential equations. Currently I am studying the book of S. J. Farlow "Partial differential equations for scientists and engineers". The attached pages show my problems. Fig. 18.4 from case two (which starts in the lower part of page 139). It shows several regions for integration concerning the problem of the wave equation with initial velocity given (1 in the interval of [-1,1]). I really have problems understanding how one obtains these six regions. If it's for the integration I would have assumed three regions and not six. Somebody knows why I am wrong?
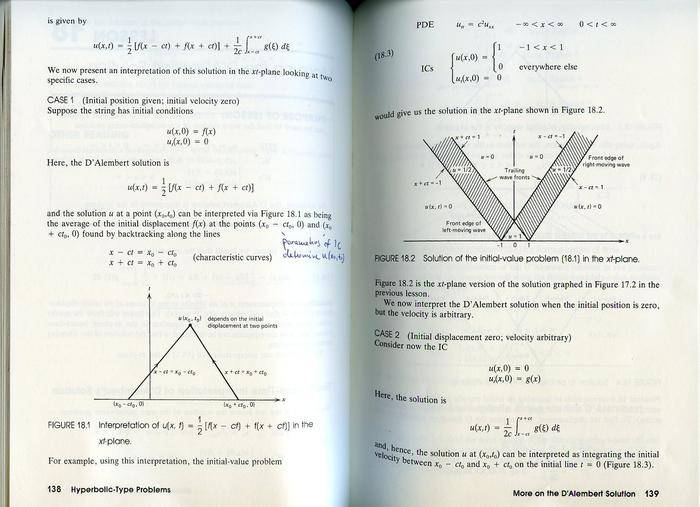

This is a problem concerning hyperbolic type partial differential equations. Currently I am studying the book of S. J. Farlow "Partial differential equations for scientists and engineers". The attached pages show my problems. Fig. 18.4 from case two (which starts in the lower part of page 139). It shows several regions for integration concerning the problem of the wave equation with initial velocity given (1 in the interval of [-1,1]). I really have problems understanding how one obtains these six regions. If it's for the integration I would have assumed three regions and not six. Somebody knows why I am wrong?