Dealing with vacuums in hydraulic systems

[deimors]

Hi,

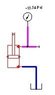
I've been trying to figure out a formula which describes the relation between the area, load and negative psig of the vacuum created in a vertical cylinder with the top port plugged and the bottom draining to tank (fig 1). I searched around for a formula describing this, and upon having no luck, decided to dive in and figure it out myself, using data I gathered from simulation software to find a decent formula.

After mucking about for a bit, I was able to come up with the equation:

P(L, A) = ((((L / (46 * A)) + 1.1)^-2) - 1) * 14.04

where P = pressure (psig), A = area (in^2) and L = load (lbs)

Now, I recognize that a complete vacuum is -14.7 psig (0 psia), but setting the horizontal asymptote at -14.04 seems to fit the curve to the data best.

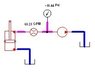
This seems all well and good to me, and so now I'm trying to deduce the pressure in situations where flow is moving in or out of the top port (as in fig 2). After some more messing about with spreadsheets, I came up with the following equation:

P(L, A, Q) = ((((L / (46 * A)) - (Q / 82.2) + 1.1)^-2) - 1) * 14.04

where Q is flow, such that positive values of Q represent flow directed into the cylinder

This seems pretty cool until I play around with it a bit and realize that there's a vertical asymptote at Q = ((L / (46 * A)) + 1.1) * 82.2.

So I suppose my question would be: is there a formula out there describing this relation that I should be using instead, or barring that (and I can't imagine this formula isn't out there _somewhere_), is there a way I could deal with this problematic asymptote?

Any help on this matter would be greatly appreciated.

 

[FredGarvin]

I may be reading this too simply, but the way I see it now, you only need to look at the volume created in the upper part of the cylinder (since diameters are constant you only really need the length of stroke). Since it has a set mass of air in the space above, the pressure will drop as that volume increases (it may help to deal with absolute pressures in stead of gauge pressures). Once you know the pressure in the volume above the cylinder, then you know what the minimum load needs to be to hold the piston in place.

Am I understanding your problem correctly?

 

[deimors]

Thanks for the reply,

I suppose I should point out that I'm dealing with hydraulics, rather than pneumatics as you appear to have interpreted the situation. Whereas there's a nice linear relation between surface area and load when dealing with situations creating positive relative pressure, the linearity breaks down when dealing with negative relative pressure. From what I've read, this is a result of attempting to expand the fluid, which will drop it below the vapor point, transitioning some of the fluid into a gas. Since the gas can occupy more space than the fluid, the volume of the mass changes, thus reducing the pressure in comparison with it's positive pressure counterpart (ie: the positive pressure created by the same load in the same vertical cylinder were the bottom port plugged rather than the top). I've attached a handy little graph showing the positive and negative pressure created by various loads for cylinders with 1,2,3 and 4 in^2 areas (although, this is graphing data gathered from a simulation, hence the strange characteristics of the curves for small loads).

Also, I'm trying to come up with a formula to determine the pressure given the load and dimensions of the cylinder, rather than determining the load required to create such a pressure. Thus, the volume of the mass is a dependent variable I'm attempting to determine (along with the others), rather than an independent variable I can use as a starting point in my calculations.

I should also point out that I am merely a humble code monkey, rather than an engineer proper, so if what I'm doing seems insane and misguided, it very well could be.