PainterGuy
- 938
- 73
- TL;DR Summary
- A function could be decomposed into even and odd parts but do those parts equally contribute to form the resultant vector?
Hi,
I understand how any function could be decomposed into even and odd parts assuming the function isn't a purely even or odd to start with.
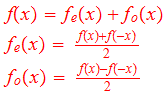
It's just like saying that any vector in x-y plane could be decomposed into its x- and y-component assuming it doesn't lie parallel to x- or y-axis. Its x-component could be 'stronger' than its y-component, or vice versa. Or, both components could be equal.
It it possible to make a similar statement about even and odd parts of a function? Is it possible that even part is dominant compared to its odd part, and so on?
Thank you!
I understand how any function could be decomposed into even and odd parts assuming the function isn't a purely even or odd to start with.
It's just like saying that any vector in x-y plane could be decomposed into its x- and y-component assuming it doesn't lie parallel to x- or y-axis. Its x-component could be 'stronger' than its y-component, or vice versa. Or, both components could be equal.
It it possible to make a similar statement about even and odd parts of a function? Is it possible that even part is dominant compared to its odd part, and so on?
Thank you!
Last edited: