- #1
parshyaa
- 307
- 19
I have seen a proof for the formula of A.B =
||A|| ||B|| cos(theta)[ proof using the diagram and cosine rule]. In the proof they have assumed that distributive property of dot product is right. diagram is given below
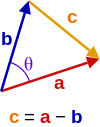 c.c =(a-b).(a-b) = a^2 +b^2 -2(a.b) [ here they used distributive law]
c.c =(a-b).(a-b) = a^2 +b^2 -2(a.b) [ here they used distributive law]
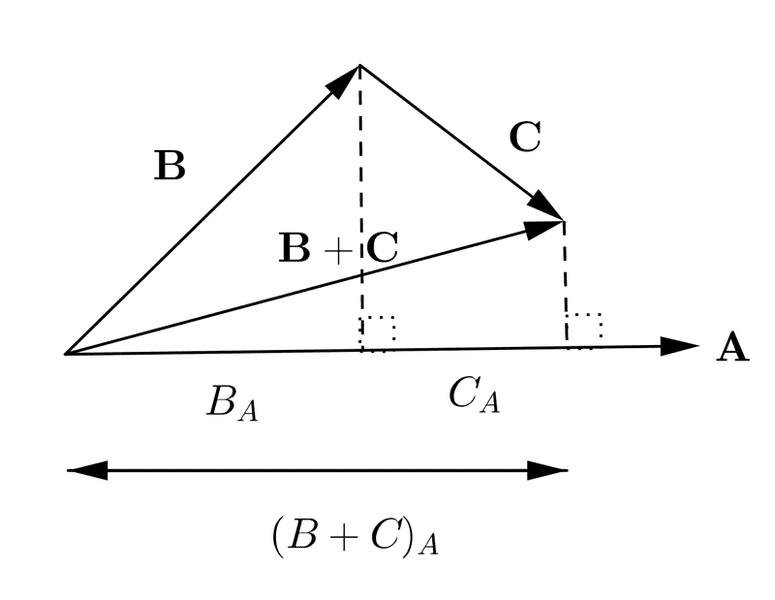
And projection of vector B on A is ||B||cos(theta) = B.a^ ( a^ is a unit vector in the direction of a vector)[ this is possible if the formula of dot product is assumed to be right.
||A|| ||B|| cos(theta)[ proof using the diagram and cosine rule]. In the proof they have assumed that distributive property of dot product is right. diagram is given below
- I have seen another proof for the distributive property of dot product. There they have assumed that A.B = ||A|| ||B|| cos(theta),And used projections. They have used the diagram as given below.
And projection of vector B on A is ||B||cos(theta) = B.a^ ( a^ is a unit vector in the direction of a vector)[ this is possible if the formula of dot product is assumed to be right.
- How they can do this , for proving dot product A.B = ||A|| ||B|| cos(theta) they have assumed distributive property to be right and for prooving distributive property they have assumed dot product to be right.
Last edited by a moderator: