- #1
metastable
- 514
- 53
Source: https://mathinsight.org/vectors_cartesian_coordinates_2d_3d
"A vector in three-dimensional space. A representation of a vector a=(a1,a2,a3)a=(a1,a2,a3) in the three-dimensional Cartesian coordinate system."
My question is does representation of a vector to arbitrary precision require 3 values? Can I represent any vector to arbitrary precision with a single value by superimposing a spiral from pole to pole on the surface of a sphere, defining north pole as 0 and south pole as 1, and referencing a point on the spiral as a percentage value. To achieve arbitrary precision I increase the number of "orbits" the superimposed spiral completes around the sphere on its path from north to south. The vector is a ray originating at the center of the sphere, crossing the surface at the referenced point on the spiral. Has this been done before and is it valid?
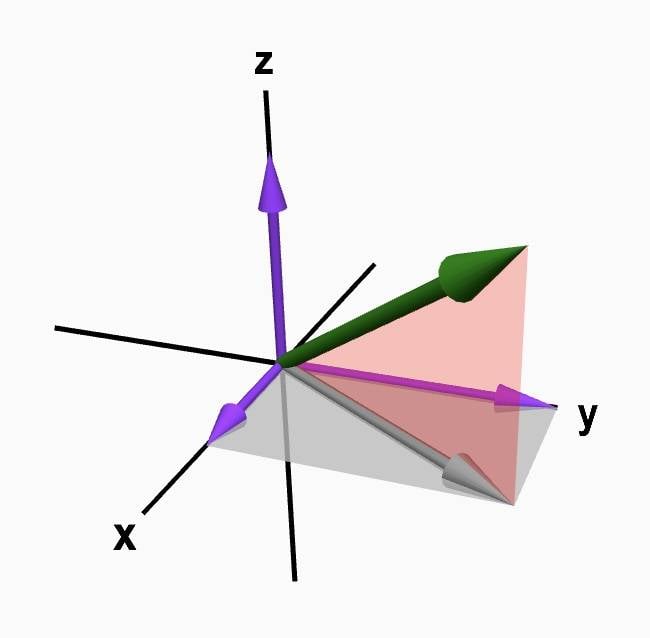
"A vector in three-dimensional space. A representation of a vector a=(a1,a2,a3)a=(a1,a2,a3) in the three-dimensional Cartesian coordinate system."
My question is does representation of a vector to arbitrary precision require 3 values? Can I represent any vector to arbitrary precision with a single value by superimposing a spiral from pole to pole on the surface of a sphere, defining north pole as 0 and south pole as 1, and referencing a point on the spiral as a percentage value. To achieve arbitrary precision I increase the number of "orbits" the superimposed spiral completes around the sphere on its path from north to south. The vector is a ray originating at the center of the sphere, crossing the surface at the referenced point on the spiral. Has this been done before and is it valid?