Derivation of Hyperbolic Representation from Lorentz/Minkowski equations in SR

[starthaus]

starthaus -

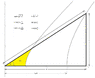
If one takes the Lorentz equatons:

$$x' = \gamma(x - vt)$$
$$t' = \gamma(t - vx)$$ where v really is $$\beta$$

and substitutes them into the Minkowski identity

$$c^2t'^2 - x'^2 = c^2t^2 - x^2$$

We wind up with an identity (either way) and a hyperbola is suggested

$$c^2t^2 - x^2 = a^2$$

This $a^2$ looks like $\tau^2$. Is that so? It doesn't make sense that $a$ would be proper time.

You previously stated an equation $$c^2 d \tau^2 = c^2 dt^2 - dx^2$$

This is clearly not the same thing.

What does the $a^2$ represent? Is there anyway of relating it to $v$ and [itex] \gamma [/tex]?

I explained all of the above https://www.physicsforums.com/blog.php?b=1911 , in my blog, there is a whole chapter dedicated to "accelerated motion in SR".

 

[Fredrik]

To anyone -

Would this be proper notation?

$$\begin{pmatrix}x' \\ t'\end{pmatrix} = \Lambda \begin{pmatrix}x \\ t\end{pmatrix}$$

$$\begin{bmatrix}x' \\ t'\end{bmatrix} = \Lambda \begin{bmatrix}x \\ t\end{bmatrix}$$

stevmg

You can write it that way, if your $\Lambda$ is

$$\begin{pmatrix}-v & 1\\ 1 & -v\end{pmatrix}$$

but I think most people prefer to have the time coordinate on top (because the coordinates are usually numbered 0,1,2,3, with 0 being the time coordinate), and

$$\Lambda=\begin{pmatrix}1 & -v\\ -v & 1\end{pmatrix}$$

It doesn't matter if you use parentheses () or square brackets []. That's just a matter of taste.

a square root with a long top bar

The "itex" tags don't work as well as they should. Many formulas get their top cut off. For example A^T, \vec V and \sqrt{2} look like this in itex tags: $A^T$, $\vec V$ and $\sqrt{2}$. Hm, that "T" looks better than it used to. If you see stuff get cut off when you preview, change the itex tags to tex tags, and consider putting the math expression on a line of its own, like this:

[tex]E=mc^2[/itex]

Then continue the text below.

 

[stevmg]

Many thanks, Fredrik

?$\Lambda= \gamma$ $$\begin{pmatrix}1 & -v\\ -v & 1\end{pmatrix}$$ $?$

stevmg

 

[stevmg]

Thanks starthaus -

I had previously downloaded that "Accelerated Motion in SR - II.pdf" file and printed it and now that I have had a better opportunity to understand the mechanics of hyperbolic transformations, I will have a better chance at digesting it.

One doesn't learn this stuff overnight.

 

[Fredrik]

Many thanks, Fredrik

?$\Lambda= \gamma$ $$\begin{pmatrix}1 & -v\\ -v & 1\end{pmatrix}$$ $?$

stevmg

Yes, I forgot the gamma.

 

[Passionflower]

In your thinking what do they represent in SR? There's an invariance but how do we use that?

Well here is where it all starts:

Think how an Euclidean space compares to a Minkowski space. Think: "circle becomes hyperbola".

Some more pictures that perhaps can help you (see pages 13, 14 and 15)
http://www.visualrelativity.com/papers/Salgado-GRposter.pdf

 

[stevmg]

Passionflower -

I downloaded that .pdf file and it is one of the most concise, descriptive and a propo descriptives I have seen.

They mention a series of articles. Were there more?

Many, many thanks,

stevmg

 

[yuiop]

Doc has expressed an interest in how the hyperbolic representation of SR relates to a purely trigonometric representation.

In the attached drawing, the following relations are illustrated on the chart on the right with the circular plots:$$sin(\theta) = \Delta x / \Delta y = v$$
$$cos(\theta) = 1 / \gamma$$
$$sec(\theta) = \gamma$$
$$tan(\theta) = \Delta x / \Delta \tau = v\gamma = w$$

where w is the proper velocity or celerity.

These can be compared to the analogous hyperbolic representations:

$$tanh(U) = v$$
$$cosh(U) = \gamma$$
$$sinh(U) = w$$

where U is twice the area shaded in yellow on the hyperbolic chart on the left and this area is proportional to the rapidity.

The slope of the brown diagonal line in the hyperbolic chart on the left is equal to the ordinary velocity, while the slope of the diagonal line in the trigonometric chart on the right, is equal to the proper velocity.

While constructing these charts I noticed the following interesting analogue between the hypotenuse in trigonometry and a quantity I will call simply hyph in hyperbolic geometry.

In trigonometry, the length of the hypotenuse is defined as:

$$\sqrt{adj^2 + opp^2}$$

In hyperbolic geometry, the analogous hyph is here defined as:

$$\sqrt{adj^2 - opp^2}$$

with the limitation that for real quantities, adj>opp.

Hyph is then where a hyperbolic curve passing through the point (x,y) = (adj,opp) intercepts the x axis, or equivalently where hyperbolic curve passing through the point (x,y) = (opp,adj) intercepts the y axis.

With the above definition, the hyperbolic functions can be represented by:

$$sinh(U) = \frac{opp}{hyph}$$

$$cosh(U) = \frac{adj}{hyph}$$

$$tanh(U) = \frac{opp}{adj}$$

which are obviously analogous to the trigometric functions:

$$sin(\phi) = \frac{opp}{hyp}$$

$$cosh(\phi) = \frac{adj}{hyp}$$

$$tanh(\phi) = \frac{opp}{adj}$$

The above relationship between hyph and hyp is illustrated in the second attached diagram.

 

[stevmg]

Doc has expressed an interest in how the hyperbolic representation of SR relates to a purely trigonometric representation.

In the attached drawing, the following relations are illustrated on the chart on the right with the circular plots:


$$sin(\theta) = \Delta x / \Delta y = v$$
$$cos(\theta) = 1 / \gamma$$
$$sec(\theta) = \gamma$$
$$tan(\theta) = \Delta x / \Delta \tau = v\gamma = w$$

where w is the proper velocity or celerity.

These can be compared to the analogous hyperbolic representations:

$$tanh(U) = v$$
$$cosh(U) = \gamma$$
$$sinh(U) = w$$

where U is twice the area shaded in yellow on the hyperbolic chart on the left and this area is proportional to the rapidity.

The slope of the brown diagonal line in the hyperbolic chart on the left is equal to the ordinary velocity, while the slope of the diagonal line in the trigonometric chart on the right, is equal to the proper velocity.

While constructing these charts I noticed the following interesting analogue between the hypotenuse in trigonometry and a quantity I will call simply hyph in hyperbolic geometry.

In trigonometry, the length of the hypotenuse is defined as:

$$\sqrt{adj^2 + opp^2}$$

In hyperbolic geometry, the analogous hyph is here defined as:

$$\sqrt{adj^2 - opp^2}$$

with the limitation that for real quantities, adj>opp.

Hyph is then where a hyperbolic curve passing through the point (x,y) = (adj,opp) intercepts the x axis, or equivalently where hyperbolic curve passing through the point (x,y) = (opp,adj) intercepts the y axis.

With the above definition, the hyperbolic functions can be represented by:

$$sinh(U) = \frac{opp}{hyph}$$

$$cosh(U) = \frac{adj}{hyph}$$

$$tanh(U) = \frac{opp}{adj}$$

which are obviously analogous to the trigometric functions:

$$sin(\phi) = \frac{opp}{hyp}$$

$$cosh(\phi) = \frac{adj}{hyp}$$

$$tanh(\phi) = \frac{opp}{adj}$$

The above relationship between hyph and hyp is illustrated in the second attached diagram.

Beautiful, ------- beautiful! Now that's what I have been looking for.