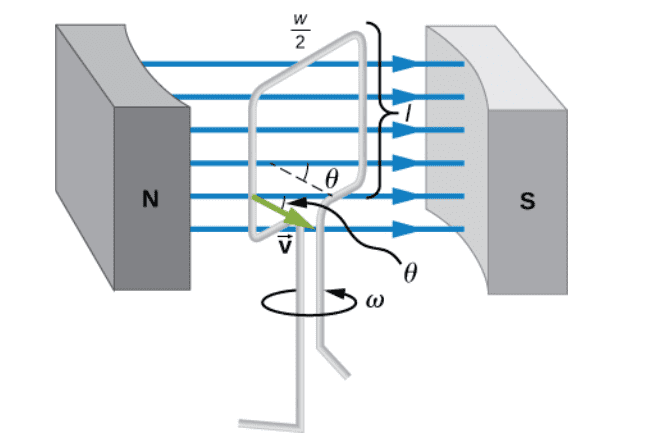
Discussion Overview
The discussion revolves around the derivation of induced voltage in a loop within a magnetic field, exploring the relationship between magnetic forces, current, and the interpretation of Ohm's Law. Participants examine the conditions under which current flows in the loop and the implications of magnetic forces acting on different segments of the loop.
Discussion Character
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- Some participants present the equation for magnetic flux and induced voltage, questioning the implications of magnetic forces being perpendicular to the loop.
- There is uncertainty about whether the sine of the angle, ##\sin\theta##, being zero is the reason for no current in certain segments of the loop.
- One participant argues that the interpretation of current in the context of the Lorentz force and electric field leads to confusion, suggesting that the motion of electrons in wires is influenced by both forces.
- Another participant emphasizes that any moving charge distribution implies a current density, challenging the notion that there is no current when magnetic forces are perpendicular.
- Participants discuss the complete form of Ohm's Law and its application in this scenario, with some expressing confusion over the presence of current density in both sides of the equation.
- There are references to the need for a more detailed explanation or visual representation to clarify the concepts being discussed.
Areas of Agreement / Disagreement
Participants express differing views on the interpretation of current flow in the loop, particularly regarding the effects of magnetic forces and the application of Ohm's Law. The discussion remains unresolved with multiple competing perspectives on the topic.
Contextual Notes
Participants note the potential for misinterpretation of textbook passages and the complexity of applying the complete form of Ohm's Law in dynamic situations. There is acknowledgment of the limitations in understanding the interactions between electric and magnetic forces in this context.