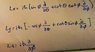You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Derivative of Lx^2+Ly^2+Lz^2 =?
- Thread starter rasi
- Start date
-
- Tags
- Derivative
AI Thread Summary
The discussion focuses on correcting the expressions for angular momentum components in a quantum mechanics context, specifically addressing errors in the terms for Lx and Lz. It is clarified that Lx should include cos(φ) instead of cot(φ), and Lz has a sign error. Participants seek to understand how to express Lx² + Ly² + Lz² in spherical coordinates. The conversation emphasizes the need for precise calculations and clarifications regarding the problem at hand. The thread highlights the importance of accuracy in mathematical expressions related to angular momentum.
Physics news on Phys.org
DrClaude
Mentor
- 8,477
- 5,693
In ##L_x##, it should be ##\cos \phi##, not ##\cot \phi##. ##L_z## has the wrong sign.
rasi
- 18
- 0
DrClaude said:In ##L_x##, it should be ##\cos \phi##, not ##\cot \phi##. ##L_z## has the wrong sign.
So how can i go on. In no way i coulnd't tackled it. Thanks for your help...
DrClaude
Mentor
- 8,477
- 5,693
Not sure what you mean here.rasi said:So how can i go on. In no way i coulnd't tackled it. Thanks for your help...
Can you describe the problem you want to solve? The title of the thread is not very clear, do you mean you need to write ##L_x^2 + L_y^2 + L_z^2## in spherical coordinates ##(\theta, \phi)##?
rasi
- 18
- 0
DrClaude said:Not sure what you mean here.
Can you describe the problem you want to solve? The title of the thread is not very clear, do you mean you need to write ##L_x^2 + L_y^2 + L_z^2## in spherical coordinates ##(\theta, \phi)##?
yes. just as you said.
DrClaude
Mentor
- 8,477
- 5,693
Then you need to calculate each term by applying it to itself, e.g.,
$$
L_z^2 = L_z L_z = -i \hbar \frac{\partial}{\partial \phi} \left( -i \hbar \frac{\partial}{\partial \phi} \right)
$$
$$
L_z^2 = L_z L_z = -i \hbar \frac{\partial}{\partial \phi} \left( -i \hbar \frac{\partial}{\partial \phi} \right)
$$
Similar threads
- Replies
- 6
- Views
- 2K
- Replies
- 4
- Views
- 2K
- Replies
- 1
- Views
- 2K
- Replies
- 3
- Views
- 2K
- Replies
- 2
- Views
- 1K
- Replies
- 1
- Views
- 2K
- Replies
- 6
- Views
- 3K
- Replies
- 1
- Views
- 2K
- Replies
- 3
- Views
- 2K
- Replies
- 1
- Views
- 2K
Hot Threads
-
Engineering Why is my output current so low in this Transconductance Amplifier cell?
- Started by arhzz
- Replies: 13
- Engineering and Comp Sci Homework Help
-
LTspice: Implementing a Single Balanced BJT Mixer
- Started by SumDood_
- Replies: 17
- Engineering and Comp Sci Homework Help
-
Max water pressure allowable on solar panels
- Started by ethanesh
- Replies: 16
- Engineering and Comp Sci Homework Help
-
Spiral scissor lift statics
- Started by carlcla
- Replies: 4
- Engineering and Comp Sci Homework Help
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 91
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math