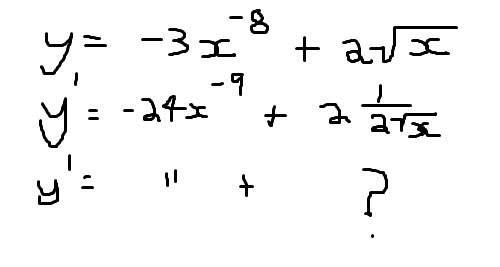How Do You Calculate the Derivative of a Function?

[laymanhobbist]

i need a bit of help ...

Suppose you want to calculate the derivative of a curve at some particular point. Draw a tangent to the curve at that point. The slope of the tangent gives you the derivative. This is geometrical approach.

The algebraical approach is little different. Let y =f(x) which means y is a function of x. A very small change in y is denoted by dy and a very small change in x is denoted by dx. The derivative of y means the amount by which y changes if x changes in a very short extent. So mathematically it is given by dy/dx.

so here ...

y = f(x) means .. that ?

 

[micromass]

I think your derivative is incorrect. It needs to be 24x^-9 instead of -24x^-9...

Anyway, what is your question??

 

[laymanhobbist]

dude , so y=f(x)

the f(x) section is the -3x^-8 + 2sqrtx ?


so the dy/dx of that is 24x^-9 ?

A very small change in y is denoted by dy and a very small change in x is denoted by dx. The derivative of y means the amount by which y changes if x changes in a very short extent. So mathematically it is given by dy/dx.

jeesus this is so ****ing confusing ...

y changes ?

x changes ?

means ... ? if the value of x changes ?

the total equation changes to something else ?

 

[Stephen Tashi]

You're quoting a non-technical description of the definition of a derivative and perhaps you need to study what "functions" are and the notations for them.

My calculus teacher illustrated the geometric version version of the derivative. He drew a graph which represented y = f(x). He pick two points A and B on the graph, which represented the points A = (a,f(a)) and B = (a+h, f(a+h)) He held a ruler between the point A and B by holding it at A with his fingers so the ruler could pivot about the point A and supported the other end of the ruler by holding his piece of chalk under it. Then he slowing moved the chalk along the curve from A to B, the ruler pivoted slowly and came to rest when the chalk go to point A. The position of the ruler defined the tangent line to the curve. (This meaning of "tangent" is not the same definition as "tangent" to a circle because it is not a statement that the tangent line must touch the curve at only one point or be perpendicular to a radius of some kind.)

This is the algebraic description of that process: The slope of the ruler is initially( f(a+h) - f(a)) / h. As we move point A to point B, the number h gets smaller and smaller and the difference f(a+h) - f(a) gets smaller and smaller. We think of h as "the small change in x" and (f(a+h) - f(a)) as the small change in y (or you can say "a small change in f " or "a small change in f(x)") You can't divide by zero so the fraction is not defined when h = 0. However there is a concept of "Limit" and "taking the limit as h approaches 0" that is part of a technically correct definition of derivative.

The above process gives you the value of the derivative when x = a, so it computes f'(a). You could imagine the point A = (x,f(x)) and B = (x+h,f(x+h)) if you prefer to see the letter 'x' instead of the letter 'a'.

You can say dx = h and dy = f(x+h) - f(x) so the derivative is often denoted as dy/dx if you prefer that to f'(x). However, in ordinary calculus, dy/dx does not denote an actual fraction and the symbols dy and dx are not numbers. dy/dx denotes the result of the process of taking the limit as h approaches 0.

The material that you quoted is non-technical. If it's from a textbook, perhaps it is merely an intutive introduction and the technicalities are taught later in the book.

 

[laymanhobbist]

functions

it keep assigning values to equation as long as it can ?

y=f(x)

point A on the x,y plane ?

and point B on the x,y plane ?
am i right till there ?

 

[Stephen Tashi]

functions

it keep assigning values to equation as long as it can ?

You need to get a book or materials that explain functions. You seem to have an intuitive understanding of the subject, but you are not using standard or precise terms to describe it.

y=f(x)

point A on the x,y plane ?

and point B on the x,y plane ?

Yes, in my example, points A and B were on the x,y plane.

 

[laymanhobbist]

this is a function that .. assigns values to x .. at definite intervals ?

yea ?and we should derive the roots ?

is that what it means by finding the derivative .. ?

are we trying to find the intervals ?mr tashi , mr tashi .. one minute ..

i took a scale .. and tried to find the slope ...

through many points ?

 

[Mark44]

I'm inserting some LaTeX code that represents your function.
f(x) = -3x^{-8} + 2x^{1/2}

this is a function that .. assigns values to x .. at definite intervals ?

For each value x in the domain of this function, the function assigns a value. The implied domain is {x | x != 0} intersected with {x | x > 0}, for the first and second terms, respectively. The intersection of these two sets is {x | x > 0}.

yea ?


and we should derive the roots ?

You can find the roots, if that's called for in a problem. I would shy away from saying "derive" the roots, because some people might interpret this (incorrectly) to mean that we are going to find the derivative.

The roots are the values of x for which f(x) = 0.

is that what it means by finding the derivative .. ?

No. Finding the derivative means finding the function that gives the slope of the tangent to the graph of f at each point in the domain of f.

For this function, f'(x) = 24x^-9 + 1/x^1/2. For example, at the point (1, -1) on the graph of f, the slope of the tangent line at that point is f'(1) = 24 + 1 = 25.

are we trying to find the intervals ?

What intervals are you talking about?

mr tashi , mr tashi .. one minute ..

i took a scale .. and tried to find the slope ...

through many points ?

 

[Stephen Tashi]

mr tashi , mr tashi .. one minute ..

i took a scale .. and tried to find the slope ...

through many points ?

That's real good that you done that, layman. Yes, that's real good that you done that. I wouldn't want to read a post that fell below your usual standards.

 

[laymanhobbist]

I'm inserting some LaTeX code that represents your function.
f(x) = -3x^{-8} + 2x^{1/2}
For each value x in the domain of this function, the function assigns a value. The implied domain is {x | x != 0} intersected with {x | x > 0}, for the first and second terms, respectively. The intersection of these two sets is {x | x > 0}.
You can find the roots, if that's called for in a problem. I would shy away from saying "derive" the roots, because some people might interpret this (incorrectly) to mean that we are going to find the derivative.

The roots are the values of x for which f(x) = 0.
No. Finding the derivative means finding the function that gives the slope of the tangent to the graph of f at each point in the domain of f.

For this function, f'(x) = 24x^-9 + 1/x^1/2. For example, at the point (1, -1) on the graph of f, the slope of the tangent line at that point is f'(1) = 24 + 1 = 25.
What intervals are you talking about?

that is a very nice explanation mr Mark44


this derivative is simply about finding the rate of slopes ..

y2-y1 / x2-x1

That's real good that you done that, layman. Yes, that's real good that you done that. I wouldn't want to read a post that fell below your usual standards.

guess what mr tashi ..

after reading and writing about a bit of slopes ..

i think differentiation is simply about finding slopes ..

between points ..

 

[Calrid]

Differentiation is simply about finding what value the slope has or will have which is given by the rate of change at any given set of points in a function. But yes basically it's all about

y=mx+c

Integration is about what is under the slope, or in a 2d case the line of the graph. I bet you can imagine that the scale of the change is related to the area of the change precisely.

That is calculus in a nut shell although of course there is much more to it than just that.

The differential of 10 is 0 because there is no slope in a horizontal line at f(x)=10. The integral of 10 is 10x because the line incorporates 10 lots of x at x=10. It's not rocket science.

So what's the volume of a square with sides measuring 10cms?

\int_0^{10} 10 \;\; dx \rightarrow 10x

so when x=10; 10x10 =100, 10x0=0; 100-0 =100cms

We usually add a constant but in this case we ignore it as there is a definite solution and we specified the units in the question.

 

[laymanhobbist]

functions are confusing me a lot ...

a function has an x , y ..

numbers ...

roots ..

trignometric stuffs .. like sinx .. sin theta ..and the thing about functions is that ..

it changes ..

whew ..

 

[Calrid]

functions are confusing me a lot ...

a function has an x , y ..

numbers ...

roots ..

trignometric stuffs .. like sinx .. sin theta ..and the thing about functions is that ..

it changes ..

whew ..

Buy a textbook high school or A' level/college depending on which part of the world you live in.

As others have said you need to start with the basics and work your way into calculus its not something you can just flip to the end and start doing.

But yes let's take speed which is in metres per second or m/s or ms^-1. We have a relation ship a dependant variable and an independent variable

ie we have distance and time dx/dt which is equal to speed.

If I increase speed then what happens to the dependant variable?

That is what calculus does in terms of differentials.

If I differentiate twice I end up with miles per second per second m/s/s or ms^-2 which conveniently are the units of acceleration, how fast I go faster to put it in simpler language. Gradient is just a rate of change it can be in time, distance, or anything really as long as there are dependant variables and independent ones.

What would I be measuring if I measured the rate of change in the rate of change of change?

It's not hard you just can't skip all the steps in between.

Sin is easy. Sin is a relationship to a triangle inside a circle. it's useful because it cycles periodically between 1 and 0 sometimes it is negative, so that you can use it to represent waves which are merely two halves of a circle which repeats. If you look at them in that way its obvious how sin relates to a simple sinusoidal wave.

If you imagine sin there changing sign as it enters different quadrants of the circle then you get a value for sin between 1 and 0 negative and positive, or more accurately in degrees between 0 and 360 and of course 720 or up to infinity as it cycles.

Think of it this way as the angle changes its relation to length is a precise value hence, it tracks the surface of the circle this is a precise value at each point hence if we know the angle we know which point of the wave or circle we are at.

Interestingly sin is equal to cosine at certain values as are many of the trig functions, hence trig identities. Which means basically if we look at the value of the wave at a certain point it is the same in cosine(x) as it is in sin(x). This underpins some rules in calculus too. in a physical wave we would say that at time t cos(x) is equivalent to sin (x). The height of a sea wave is 1 m at the point where I am standing at 0 seconds, 10 seconds and 20 seconds. Another seawave is equal to 1m at -1/2,1/2,1 and1/2 periods in time hence we can say that their sin and cos values are equal at certain points. Or to put it in maths jargon and using the rate of change:

\frac{d}{dx} \sin(x) = \cos(x)

The rate of change of sin(x) or the derivative of sin(x) is equivalent to cos (x).

If we placed this relationship on the graph above we would create a wave that was exactly the same as another wave but at different moments in time. It would actually look a bit like a series of circles in the graph as they are opposing each other.

 

[Mark44]

that is a very nice explanation mr Mark44

this derivative is simply about finding the rate of slopes ..

y2-y1 / x2-x1

That's more or less the idea.
Some corrections -
The derivative of a function is another function that gives the slope of the line that is tangent to the graph of the first function.

You're not finding the "rate of slopes" - the derivative already is a rate; the rate of change of the function's y values relative to the change in x values.

The ratio you wrote, "y2 - y1 / x2 - x1" represents the slope of a secant line on the graph of whatever function we're talking about. This is a line segment that intersects two points on the graph of our function. The two points are (x1, y1) and (x2, y2). A tangent line at a point on the graph of a function is a line that touches just that point. (It's possible for the tangent line to intersect the graph at some other points, though.)

BTW, this ratio, which is usually called the difference quotient, should be written with parentheses around the numerator and denominator, like this: (y2 - y1)/(x2 - x1). Without the parentheses, this expression would be interpreted to mean y2 - (y1/x2) - x1, which I'm sure isn't what you meant.

An example might help your understanding. Let f(x) = x². I think you understand enough about the mechanics of differentiation to see that the derivative function is f'(x) = 2x.

Two points on the graph of f are (1, 1) and (2, 4). The slope of the secant line between these two points is (4 - 1)/(2 - 1) = 3/1 = 3.

The slope of the tangent line at x =1 is the value of the derivative function at x = 1; namely f'(1) = 2(1) = 2.

Why the difference?

The derivative of a function at a number x = a is defined as the limit of the slope of the secant line, as x approaches a. In mathematical terms, we have
f'(a) = \lim_{x \to a} \frac{f(x) - f(a)}{x - a}

If we're trying to find the slope of the tangent line to our function (f(x) = x²) at x = 1, then a = 1 and f(a) = 1 in the formula above, so we have
f'(1) = \lim_{x \to 1} \frac{f(x) - f(1)}{x - 1} = \lim_{x \to 1} \frac{f(x) - 1)}{x - 1}

It's possible to work with this limit to come up with the exact value for f'(1), but I'm not sure your present skills are up to it. Instead, let's take a few points that are get successively closer to (1, 1) and calculate the slope of the secant line.

1. x = 1.5, f(1.5) = (1.5)² = 2.25
slope of secant line = (2.25 - 1)/(1.5 - 1) = 1.25/.5 = 2.5
2. x = 1.1, f(1.1) = (1.1)² = 1.21
slope of secant line = (1.21 - 1)/(1.1 - 1) = .21/.1 = 2.1
3. x = 1.01, f(1.01) = (1.01)² = 1.0201
slope of secant line = (1.0201
- 1)/(1.01 - 1) = .0201/.01 = 2.01

Hopefully, you get the idea. As x gets closer to 1, the slope of the secant line seems to be getting closer to 2, which we have calculated to be the slope of the tangent line at the point (1, 1) - IOW, f'(1).

guess what mr tashi ..

after reading and writing about a bit of slopes ..

i think differentiation is simply about finding slopes ..

between points ..

 

[Nicook5]

functions are confusing me a lot ...

a function has an x , y ..

numbers ...

roots ..

trignometric stuffs .. like sinx .. sin theta ..and the thing about functions is that ..

it changes ..

whew ..

a mathematical function simply relates input to output. In a function each input has only one output. x and y are just variables, you can replace them with and numbers, but generally x is used as an input and y is the output, or f(x) (a function can also have more than one input). roots just generally refer to what inputs would make the output equal to 0.