Derive Relative Intensities from LS-Coupling Sum Rules

[John Greger]

Homework Statement

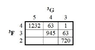
The table gives the theoretical relative intensities in LS-coupling for all possible $^3F – ^3G$ transitions.

a) Use this data to verify the sum rules for

LS-intensities in a multiplet.
b) Use the sum rules to derive the relative intensities in a $^2D – ^2F$ multiplet. Hint: denote the intensities a, b and c and solve a system of equations.

Homework Equations

$\Sigma I / g = constant$. Where g=2J + 1

The Attempt at a Solution

So in a it was easy to verify the sum rule above. By simply summing the intensities for each column/row divide by 2J + 1 and se that the values was constants for the columns and rows.

However, in b). I sat up the equations $$a+b = 8*D_1$$
$$c = 8*6_1$$ and $$a+b = 10*D_2$$ $$b+c = 8*D_2$$

But I have to many unknown variables here. D1 and D2 is the constants for the rows and columns, respectively.

But perhaps D1 and D2 are the same as they where for the tripplet G and F, because then the problem is very simple. (I have no solutions so I don't know the right answer).

 

[Nate810]

Any help would be appreciated. A:Your equations are correct but you are missing the constants from the sum rules. $\sum_{i} \frac{I_{i}(J)}{2J+1} = k$ where k is a constant. Since you have a 2F, 3G multiplet you can use this equation twice to get two equations with two unknowns. The equation for the 2F multiplet is $\frac{a+b}{3} = \frac{2}{7}$ and the equation for the 3G multiplet is $\frac{a+b+c}{5} = \frac{3}{13}$ which should give you the solution.