Deriving Formula for Radius of Conical Section at Height h

[zorro]

Homework Statement

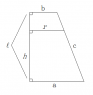
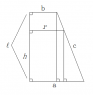
Suppose there is a Conical section (of a right circular cone) of total height 'l' and radii 'a' and 'b' (a>b). How do we derive the formula for the radius at a height 'h' (h<l) ?

Homework Equations

The Attempt at a Solution

 

[pongo38]

Draw a cross section through the middle and look for similar triangles whose properties you can use to solve your problem. (I think you are describing a frustrated cone, not a pure cone?)

 

[zorro]

I am talking about this (see attached file).

 

[Mark44]

Draw a cross section through the middle and look for similar triangles whose properties you can use to solve your problem. (I think you are describing a frustrated cone, not a pure cone?)

Good advice, but the term is "frustum of a cone."

 

[zorro]

Good advice, but the term is "frustum of a cone."

Haha (or in other words, a truncated cone)
How was his advice good? We can't use similar triangle property to find the radius.

 

[Mark44]

Extend the vertical line at the center and the outer sloped line up until they meet, then you'll have similar triangles.

 

[zgozvrm]

Forget the 3 dimensional aspect; it would be easier to think of a trapezoid with one side of length [itex]l[/tex], perpendicular to sides a & b. Call the remaining side c.<br /> <br /> a & b still represent the upper and lower radii of your truncated cone, and r represents the radius of that object at height <i>h</i> above side a.[/itex]

 

[zgozvrm]

Extend the vertical line at the center and the outer sloped line up until they meet, then you'll have similar triangles.

I find the algebra easier if you construct the additional 2 line segments shown in the attached drawing.

 

[zorro]

Thanks a lot zgozvrm. I got my answer

 

[zgozvrm]

Glad to help.

What did you come up with?

 

[zorro]

r = a - h(a-b)/l

 

[zgozvrm]

Very nice!