Deriving motion equations for two blocks on a rough table

[TonyV]

Two small blocks, each of mass m, are connected by a string of constant length 4h and negligible mass. Block A is placed on a very rough tabletop as shown below, and block B hangs over the edge of the table. The tabletop is a distance 2h above the floor. Block A is then released from rest at a distance h above the floor at time t = 0 and the system begins to move. The coefficient of kinetic friction is μk.
Express all algebraic answers in terms of μk, h, m1, m2, , and g.

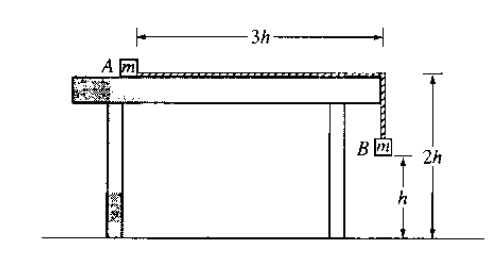
A) Write equations for the sum of forces in both directions.
From what I understand, the sum of all forces would be ΣF = (sum of forces) = ma.

B) Derive an equation for the acceleration of block B as it descends.
I thoughtlessly did this without accounting for friction and ended up with g/2. I did a similar problem for homework and was used that information to come up with this equation for acceleration... However, I am unsure of whether or not I am on the right path.

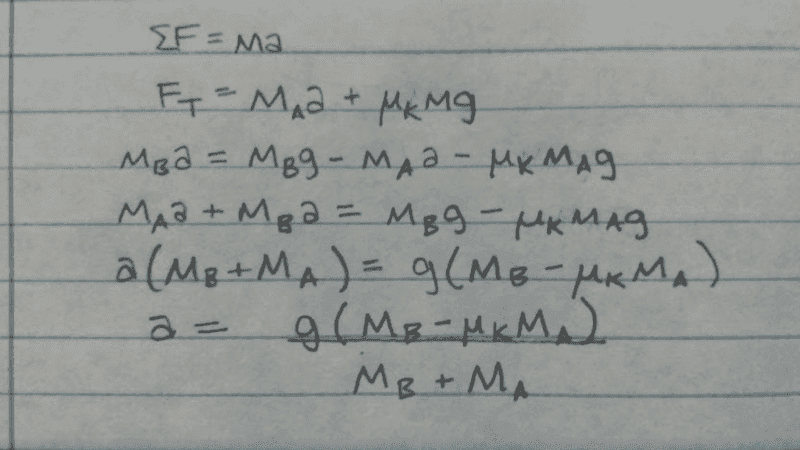
I would end up with variables canceling out in the final equation, correct??

C) Block B strikes the floor and does not bounce. Determine the time t at which block B strikes the floor.
For this I ended up with 2√h/g. However, since I got this equation by substituting acceleration with the equation from the previous step (g/2) in h=½at^2. I am unsure of how to proceed until I am certain of what I need to use for acceleration to solve for time.

I am grateful for any assistance and/or suggestions. I love physics but still have much to learn! However, I want to understand as much as possible.

 

[mfb]

There is a coefficient of friction given. You can't neglect friction.

 

[haruspex]

unsure of how to proceed until I am certain of what I need to use for acceleration to solve for time.

Your second attempt at acceleration was correct. It is not unusual that some variables cancel out. In the present case, would you expect the acceleration or time to be different if both masses were doubled?

 

[TonyV]

Your second attempt at acceleration was correct. It is not unusual that some variables cancel out. In the present case, would you expect the acceleration or time to be different if both masses were doubled?

Thank you... In this particular case no. At least I am pretty sure it is irrelevant in this case. So in the equation for a, both of my mass variables would cancel out? That would leave me with g(-μk)

 

[TonyV]

There is a coefficient of friction given. You can't neglect friction.

The previous problem had negligible friction... This is why it's important to read the entire problem before attempting to solve.

 

[haruspex]

That would leave me with g(-μk)

No. Starting with the last equation in the image you posted, and setting the two masses equal, please post your steps.

 

[TonyV]

Okay, here is what I have...

 

[haruspex]

Okay, here is what I have...

That's what you posted before, but you know the two masses are equal, so what does it simplify to?

 

[TonyV]

That's what you posted before, but you know the two masses are equal, so what does it simplify to?

2m

 

[haruspex]

2m

Eh?
No. Take the final expression in the image you posted and use the fact that the two masses are equal. (You are told this.). What does that expression then simplify to?

 

[TonyV]

Eh?
No. Take the final expression in the image you posted and use the fact that the two masses are equal. (You are told this.). What does that expression then simplify to?

Sorry, been a long week. Midterms. I know it's probably right in front of my face, obvious but I'm not seeing much else... Unless it cancels out...

 

[haruspex]

Sorry, been a long week. Midterms. I know it's probably right in front of my face, obvious but I'm not seeing much else... Unless it cancels out...

I cannot understand your difficulty. You had $a=g\frac{M_B-\mu_kM_A}{M_B+M_A}$. Just replace each M_A and M_B with m and simplify.