Aleoa
- 128
- 5
I'm trying to derive the lever law by myself, however, I'm stuck. Please follow the logic of my calculations.

Every object in the picture has the same mass. I want to prove that, under the effect of the gravitational force, I can replace the objects in A and C with the two objects in B, and obtain a system that behaves in the same way.
Since the same gravitational force acts in the objects, in an infinitesimal time interval dt they all get the same dv. However, the correspondent infinitesimal change in angular velocity also depends on the distance between the object(s) and the fulcrum.
If i prove that in an dt the d\omega due to the objects in A and C is equal to the d\omega due to the two objects on B, I'm done.
d\omega_{A}+d\omega_{C}=d\omega_{B}
that is
\frac{dv}{OA}+\frac{dv}{OA+D}=\frac{2dv}{OA+\frac{D}{2}}
where O is the fulcrum and D is the distance between C and A.
However, doing some calculations i found that...
\frac{dv}{OA}+\frac{dv}{OA+D}\neq\frac{2dv}{OA+\frac{D}{2}}
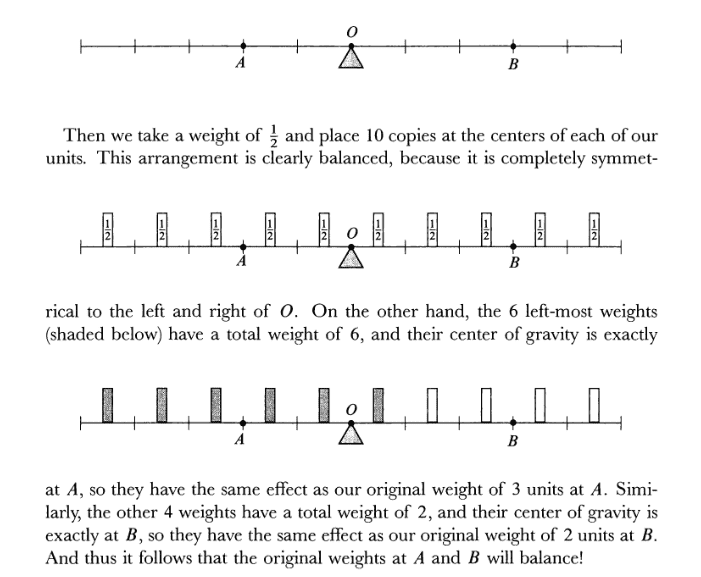
Maybe two single masses in A and C have not the same effect as a double mass in B, however according to Spivak:
Every object in the picture has the same mass. I want to prove that, under the effect of the gravitational force, I can replace the objects in A and C with the two objects in B, and obtain a system that behaves in the same way.
Since the same gravitational force acts in the objects, in an infinitesimal time interval dt they all get the same dv. However, the correspondent infinitesimal change in angular velocity also depends on the distance between the object(s) and the fulcrum.
If i prove that in an dt the d\omega due to the objects in A and C is equal to the d\omega due to the two objects on B, I'm done.
d\omega_{A}+d\omega_{C}=d\omega_{B}
that is
\frac{dv}{OA}+\frac{dv}{OA+D}=\frac{2dv}{OA+\frac{D}{2}}
where O is the fulcrum and D is the distance between C and A.
However, doing some calculations i found that...
\frac{dv}{OA}+\frac{dv}{OA+D}\neq\frac{2dv}{OA+\frac{D}{2}}
Maybe two single masses in A and C have not the same effect as a double mass in B, however according to Spivak: