Describe the final position of the weights

[matrix_204]

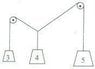
i don't understand this question, it says, three masses of 3 kg, 4kg, and 5kg, are attached to strings as shown in the diagram. The weights are released and the system reaches equilibrium. Describe the final position of the weights.
If it's in equilibrium, the weights are in a still position right. or is there a trick to this problem.

 

[ahrkron]

They are asking you for the angles og the string. Think what happened if the weight in the middle was much lighter or much heavier: the string would be almost straight or make a smaller angle, respectively. The given weights are enough information for you to calculate all angles in the diagram.

 

[HallsofIvy]

originally posted by ahrkron
The weights are released and the system reaches equilibrium. Describe the final position of the weights.
If it's in equilibrium, the weights are in a still position right. or is there a trick to this problem.

I don't see why you would think there is any trick. If the weights weren't in a "still position", it wouldn't make sense to ask you to find "the final position".

 

[Mathechyst]

IMO, the question is vague after looking at the diagram. As ahrkron pointed out, the only thing one could calculate in the angles.

Doug