- #1
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Designing a 2-bit full adder using nothing but NAND gates?
In summary: I skimmed and missed that point. And thank you that saves some brain strain!In summary, your design is for a 1 bit half adder followed by a 1 bit full adder. A two bit adder needs a carry input to make it a “full” adder. Full adders need 5 inputs in decimal, 1+3+3=7. With 3 or more inputs, no gates can be used.
Engineering news on Phys.org
- #2
mfb
Mentor
- 37,125
- 13,966
I don't see how. Check your Cout, however. If b1 is zero, your carry is always on.
- #3
ISamson
Gold Member
- 438
- 151
Does it do addition? Is that what you mean by 'adder'?
- #4
Svein
Science Advisor
- 2,298
- 796
- #5
Crushforce
- 4
- 0
Yeah I just realized that, how about this?mfb said:I don't see how. Check your Cout, however. If b1 is zero, your carry is always on.
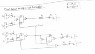
While that is a 2-bit adder it is designed with gates other than NAND. Granted I could simply replace each gate with the NAND equivalent, I kinda want to make this with the least amount of gates possible. Which is why I have come to this forum to see if I can get this simplified as much as possible.Svein said:
Attachments
- #6
Svein
Science Advisor
- 2,298
- 796
Are you familiar with Karnaugh diagrams? ( https://en.wikipedia.org/wiki/Karnaugh_map )Crushforce said:While that is a 2-bit adder it is designed with gates other than NAND. Granted I could simply replace each gate with the NAND equivalent, I kinda want to make this with the least amount of gates possible. Which is why I have come to this forum to see if I can get this simplified as much as possible.
- #7
Crushforce
- 4
- 0
Slight update there should be a not gate where it says "carry-out"
Somewhat... but not entirely. I've seen them online but I have no formal experience other than reading them.Svein said:Are you familiar with Karnaugh diagrams? ( https://en.wikipedia.org/wiki/Karnaugh_map )
- #8
Svein
Science Advisor
- 2,298
- 796
I asked because a Karnaugh map is used for minimizing logical expressions with respect to gates.Crushforce said:Somewhat... but not entirely. I've seen them online but I have no formal experience other than reading them.
Anyhow - check out https://en.wikipedia.org/wiki/Adder_(electronics) .
- #9
jerromyjon
- 1,244
- 189
I think the main point was to use only NAND gates since they can perform the function of any gate...
- #10
donpacino
Gold Member
- 1,439
- 285
Yes, You use the kmap to get the minimum logical expression, you then convert them to nand gates. You can also use the kmap and OLNY find nand gate connectionsjerromyjon said:I think the main point was to use only NAND gates since they can perform the function of any gate...
- #11
jerromyjon
- 1,244
- 189
Sorry, I skimmed and missed that point. And thank you that saves some brain strain!donpacino said:You can also use the kmap and OLNY find nand gate connections
- #12
donpacino
Gold Member
- 1,439
- 285
Happens to the best of usjerromyjon said:Sorry, I skimmed and missed that point. And thank you that saves some brain strain!
Crushforce said:Yeah I just realized that, how about this?
A good way to organize this in the future, make a block consisting of 2 inputs, 1 carry in bit, 1 output, and 1 carry out.
This will then scale to any number of bits. you just attach the carry out from one to the carry in from another. Then if you want to optimize, remove the carry in section from your first bit (although in a real system you might need it).
- #13
Baluncore
Science Advisor
2023 Award
- 14,426
- 8,319
Your design is for a 1 bit half adder followed by a 1 bit full adder.Crushforce said:I wanted to ask if there was any way that I could make it with less logic gates?
A two bit adder needs a carry input to make it a “full” adder.
Your solution, 4 inputs; in decimal, 3+3 = 6; which needs three outputs.
A full adder, 5 inputs; in decimal, 1+3+3 = 7; which also needs three outputs.
We need to know the rules of the challenge, what is the target technology?
Is there a carry input to the first stage?
Is the design restricted to using NAND gates only?
Can gates with three or more inputs be used?
- #14
Crushforce
- 4
- 0
Baluncore said:Your design is for a 1 bit half adder followed by a 1 bit full adder.
A two bit adder needs a carry input to make it a “full” adder.
Your solution, 4 inputs; in decimal, 3+3 = 6; which needs three outputs.
A full adder, 5 inputs; in decimal, 1+3+3 = 7; which also needs three outputs.
We need to know the rules of the challenge, what is the target technology?
Is there a carry input to the first stage?
Is the design restricted to using NAND gates only?
Can gates with three or more inputs be used?
1) We need to know the rules of the challenge, what is the target technology?
-There is no target tech, simply creating it using 7400 integrated circuits on a bread board.
2) Is there a carry input to the first stage?
-I'll get back to you on this.
3)Is the design restricted to using NAND gates only?
-Yes
4)Can gates with three or more inputs be used?
-No
Sorry I cannot reply to everyone, I've gotten a bit busy. I am still reading what people have to say though.
- #15
Baluncore
Science Advisor
2023 Award
- 14,426
- 8,319
When only NAND gates with two inputs are used, the fundamental 3-input EXOR gates and 3-input MAJority gates can be constructed. Each pair of those 3-input gates makes a one bit slice of full adder with ripple carry, in and out.
A two bit full adder can be made using 4 of those constructed 3-input gates.
A total of 28 primitive 2-input NAND gates are needed.
That can be reduced to 26 since one NAND gate is duplicated between the EXOR and MAJ gates.
The 74x00 chip is a Quad 2-input NAND gate. There is an alternative quad 2-input NAND that has open-collector outputs, which can be used for negative-logic wired-OR, the 74x01. It would reduce the total gate count, which is why it was quickly introduced, immediately after the 74x00.
There is a trick that can generate carry from the three input EXOR gate without need for the MAJ gate. Here is my two bit full adder, with carry in and out, that seems to work, but needs only 18 primitive NAND gates.
A two bit full adder can be made using 4 of those constructed 3-input gates.
A total of 28 primitive 2-input NAND gates are needed.
That can be reduced to 26 since one NAND gate is duplicated between the EXOR and MAJ gates.
The 74x00 chip is a Quad 2-input NAND gate. There is an alternative quad 2-input NAND that has open-collector outputs, which can be used for negative-logic wired-OR, the 74x01. It would reduce the total gate count, which is why it was quickly introduced, immediately after the 74x00.
There is a trick that can generate carry from the three input EXOR gate without need for the MAJ gate. Here is my two bit full adder, with carry in and out, that seems to work, but needs only 18 primitive NAND gates.
Code:
c1 ' carry input, bit value 1
a1, b1 ' data inputs, bit value 1
a2, b2 ' data inputs, bit value 2
c2 ' internal carry, bit value 2
s1, s2, s4 ' sum output terms, s4 is carry out
t11 = NAND( a1, b1 )
t12 = NAND( t11, b1 )
t13 = NAND( a1, t11 )
t14 = NAND( t12, t13 )
t15 = NAND( c1, t14 )
t16 = NAND( t14, t15 )
t17 = NAND( c1, t15 )
s1 = NAND( t16, t17 ) ' sum, bit value 1
c2 = NAND( t11, t15 ) ' internal carry
t21 = NAND( a2, b2 )
t22 = NAND( t21, b2 )
t23 = NAND( a2, t21 )
t24 = NAND( t22, t23 )
t25 = NAND( c2, t24 )
t26 = NAND( t24, t25 )
t27 = NAND( c2, t25 )
s2 = NAND( t26, t27 ) ' sum, bit value 2
s4 = NAND( t21, t25 ) ' sum or carry out, bit value 4
Last edited:
- #16
Vitro
- 130
- 47
@Crushforce, I think you just need one more NAND in the diagram from post 5 to invert the carry from bit 0, so you'll need 14 gates total for your 2-bit adder. But this is not a full 2-bit adder because it doesn't have a carry in, your bit 0 is a half adder, so you can't chain them to make an arbitrary length adder. That's ok though if you only need two bits and want to minimize the number of gates used.
1. How do I design a 2-bit full adder using only NAND gates?
To design a 2-bit full adder using only NAND gates, you will need to use a combination of logic gates and Boolean algebra. First, you will need to break down the 2-bit addition into smaller parts, such as the sum and carry calculations for each bit. Then, you can use NAND gates to implement these calculations according to Boolean expressions that represent the logic behind each calculation.
2. What are the benefits of using only NAND gates in the design of a 2-bit full adder?
Using only NAND gates in the design of a 2-bit full adder can reduce the number of components needed, which can save space and cost. It also allows for simpler circuitry and easier troubleshooting, as NAND gates are universal gates that can be used to implement any other logic gate.
3. What is the truth table for a 2-bit full adder using only NAND gates?
The truth table for a 2-bit full adder using only NAND gates will have two inputs for each bit (A and B), two outputs for each bit (Sum and Carry), and four rows to represent all possible combinations of inputs. The truth table will show the output values for each combination of inputs, and these values can be used to determine the Boolean expressions needed to implement the 2-bit full adder using NAND gates.
4. Can I use any other types of logic gates in addition to NAND gates in the design of a 2-bit full adder?
Yes, you can use other types of logic gates in addition to NAND gates in the design of a 2-bit full adder. However, using only NAND gates can simplify the design and reduce the number of components needed. You can also use other universal gates, such as NOR gates, to implement a 2-bit full adder.
5. How can I test the functionality of my 2-bit full adder design using only NAND gates?
To test the functionality of your 2-bit full adder design using only NAND gates, you can use a circuit simulator or a prototyping breadboard to physically build the circuit. Then, you can input different combinations of binary numbers and compare the output with the expected results from the truth table. You can also use Boolean algebra to verify the functionality of your design.
Similar threads
-
Engineering and Comp Sci Homework Help
- Replies
- 5
- Views
- 2K
-
Programming and Computer Science
- Replies
- 1
- Views
- 672
-
Electrical Engineering
- Replies
- 4
- Views
- 3K
-
Electrical Engineering
- Replies
- 6
- Views
- 6K
-
Electrical Engineering
- Replies
- 3
- Views
- 2K
-
Engineering and Comp Sci Homework Help
- Replies
- 6
- Views
- 17K
-
Electrical Engineering
- Replies
- 6
- Views
- 1K
-
Engineering and Comp Sci Homework Help
- Replies
- 2
- Views
- 1K
-
Electrical Engineering
- Replies
- 4
- Views
- 2K
-
Electrical Engineering
- Replies
- 6
- Views
- 843
Share: