_Greg_
- 36
- 0
Iv done an experiment with a spring wher you add mass and record the new length. From a table of these rusults iv plotted length (m) against mass (kg), like so
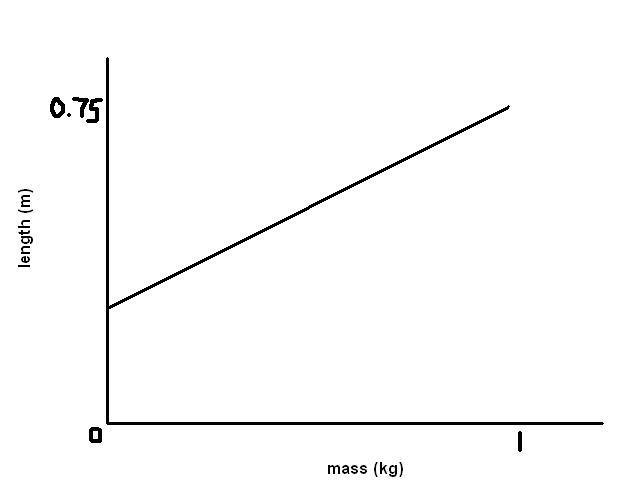
Now i have to calculate the stiffness, k, from this graph with the equation:
mg = k (l - lo)
so just to varify that what iv done is correct:
mg = (x2 - x1) x g
(l - lo) = (y2 - y1)
so k = ( (x2-x1) x g ) / (y2 - y1)
im pretty sure that's correct, its almost identical from using a single value of length and mass from the table of results.
QUESTION
how do i calculate the uncertainty in k?
all my measurements of length have an uncertainty of +/-0.5mm, each of the 100g masses i use in the experiment have an uncertainty of +/- 5g and of cource there will be an uncertainty in drawing my graph.
how do i use these to get my error in k?
btw the spring has negligible mass.
iv been trying to work this out for hours to no avail and its GOT to be in TOMORROW
any help, id really appreciate it.
Now i have to calculate the stiffness, k, from this graph with the equation:
mg = k (l - lo)
so just to varify that what iv done is correct:
mg = (x2 - x1) x g
(l - lo) = (y2 - y1)
so k = ( (x2-x1) x g ) / (y2 - y1)
im pretty sure that's correct, its almost identical from using a single value of length and mass from the table of results.
QUESTION
how do i calculate the uncertainty in k?
all my measurements of length have an uncertainty of +/-0.5mm, each of the 100g masses i use in the experiment have an uncertainty of +/- 5g and of cource there will be an uncertainty in drawing my graph.
how do i use these to get my error in k?
btw the spring has negligible mass.
iv been trying to work this out for hours to no avail and its GOT to be in TOMORROW

any help, id really appreciate it.