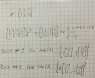Bobman
- 15
- 6
Homework Statement
[/B]
A=##\begin{bmatrix}
1 & 2 & 3 \\
4 & 8 & 12
\end{bmatrix}##
Question: Determine a basis for ker(A).
Homework Equations
Ker(A)=##\begin{bmatrix}
1 & 2 & 3& |&0 \\
4 & 8 & 12& |&0
\end{bmatrix}##
(And reduce with gaussian elimination)
The Attempt at a Solution
(Sorry for no attempt on LaTeX here, it's my first time trying to use it at all above.)
Some background information, i am revisiting linear algebra and I were doing gram-schmidt process and got a totally different answer than the textbook, however i am confident i did not make a mistake during the actual gram-schmidt.
Then it occurred to me that i must have chosen a different basis than the textbook, which made me unsure in what i recall and know about the basis for the kernel. I couldn't really find any straight forward information about it in my textbook or with a few google searches, so now I've gotten caught up in my own minor insecurities in basic details.
A easy example below to illustrate my point, are both Basis #1 and Basis #2 correct (i just realized that i wrote base on the paper...)? They would of course lead to two very different orthogonal basis when using gram-schmidt, but both would be orthogonal nonetheless.
My reasoning behind them being equally correct is that there is no (to me) intuitive "basis vector 1 and basis vector 2" as it would be for example unit vectors. Still, the span should be independent of the order in the "set" anyway if i am not wrong? I.e. i would still reach all the points regardless of the order.